ИССЛЕДОВАНИЕ СВОЙСТВ ФЕРРИМАГНИТНЫХ МАТЕРИАЛОВ

Цель работы: исследовать влияние температуры на магнитную проницаемость феррита и определить точку Кюри.

Любое вещество, помещенное в магнитное поле, приобретает магнитный момент. Возьмём катушку и будем помещать в неё сердечники из разных материалов. Магнитное поле, возникающее внутри сердечника, будет усиливать или ослаблять внешнее поле.

Намагниченность сердечника под влиянием внешнего поля можно охарактеризовать уравнением

B = μ_о ∙μ_r ∙H,

где В – магнитная индукция, Тл; μ_o – магнитная постоянная , μ_o = 4π·10^-7 Гн/м; μ_r – относительная магнитная проницаемость, о. е.

По магнитным свойствам все материалы можно разделить на две группы:

− слабомагнитные (μ_r ≈ 1);

− сильномагнитные (μ_r >> 1).

У слабомагнитных материалов μ_r = const, т.е. она не зависит от напряжённости внешнего поля. Слабомагнитные материалы можно разделить на диамагнетики (μ_r < 1) и парамагнетики (μ_r > 1).

При помещении в магнитное поле диамагнетики намагничиваются противоположно направлению внешнего поля и ослабляют его (μ_r < 1). После снятия внешнего поля индуцированный момент исчезает. К диамагнетикам относятся водород, большинство органических соединений, ряд металлов: медь, серебро, золото, цинк.

Парамагнетики намагничиваются в направлении внешнего поля и усиливают его (μ_r > 1). К парамагнетикам относятся кислород, щелочные металлы, алюминий, платина и т. д.

Слабомагнитные материалы в технике применяются редко.

У сильномагнитных материалов μ_r >>1 и зависит от напряжённости внешнего поля. Эти материалы используются в энергетике в качестве магнитных материалов. К ним относятся железо, никель, кобальт, их сплавы, ферриты.

Относительная магнитная проницаемость обозначается символом μ_r, но в лабораторной работе для удобства обозначения индекс r опущен.

Сильномагнитные материалы можно разделить на две группы:

− ферромагнитные (железо, никель, кобальт и их сплавы);

− ферримагнитные (ферриты: магнитная керамика, окислы металлов).

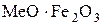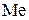Ферриты – это неметаллические магнитные материалы, обладающие большим электрическим сопротивлением (в 10⁶–10¹¹ раз большим, чем у электротехнической стали) и высокой относительной магнитной проницаемостью (до 10 000). Ферриты представляют собой системы из окислов железа и окислов двухвалентных, реже – одновалентных металлов, соответствующие общей формуле , где – символ двухвалентного металла. Их магнитные свойства обусловлены внутренними скрытыми формами движения электрических зарядов, представляющими собой элементарные круговые токи. Такими круговыми токами являются вращение электронов вокруг собственных осей (электронные спины) и орбитальное вращение электронов в атомах. Явление ферримагнетизма связано с образованием внутри некоторых материалов ниже определенной температуры (точки Кюри) таких кристаллических структур, при которых в пределах макроскопических областей, называемых доменами, электронные спины оказываются ориентированными параллельно друг другу и одинаково направленными. Таким образом, характерным для ферримагнитного состояния вещества является наличие в нем самопроизвольной, или спонтанной намагниченности без приложения внешнего магнитного поля.

Магнитная проницаемость ферромагнитных материалов зависит от температуры. При увеличении температуры облегчается переориентация доменов по полю и магнитная проницаемость растёт, но при температуре выше определённого значения, называемого точкой Кюри (Тк), происходит разрушение доменной структуры и магнитные материалы теряют свои ферромагнитные свойства. На рисунке 7.1 приведена типичная зависимость магнитной проницаемости от температуры.

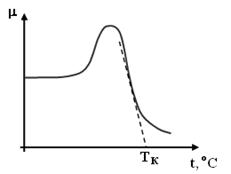
Рис. 7.1. Зависимость магнитной проницаемости ферритов от температуры

В лабораторной работе № 7 определяется точка Кюри ферримагнитного материала. Ферримагнитный материал выбран потому, что у большинства этих материалов точка Кюри ниже 400 ^оС и ее несложно определить в лабораторных условиях. А у ферромагнитных материалов она гораздо выше. Так, для чистого железа точка Кюри составляет 768 ^оС, для никеля 358 ^оС, для кобальта 1131 ^оС.

Для характеристики изменения магнитной проницаемости от температуры пользуются температурным коэффициентом магнитной проницаемости:

TK_μ = ,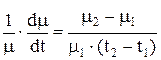

где TK_m – температурный коэффициент, град^-1; m₁ и m₂ – магнитные проницаемости при температурах t₁ и t₂ соответственно, причем t₂ > t₁.

Эту лабораторную работу можно выполнять на экспериментальной установке (ч. 1, рис. 7.2).

Для этого необходимо измерить цифровым прибором АМ-3003 индуктивность однослойной катушки, равномерно намотанной на ферритовый сердечник.

Магнитная проницаемость такого сердечника рассчитывается по формуле

μ = ^,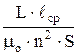

где L – измеренная индуктивность, Гн; n – число витков катушки (n = 100);
S – площадь сечения сердечника (рис. 7.2), м²; 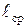– средняя длина магнитопровода, м; μ_o – магнитная постоянная (μ_o = 4π·10^-7 Гн/м).

Рис. 7.2. Размеры сердечника

Площадь сечения сердечника равна

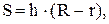
где h – толщина сердечника, h = 6 мм; R – внешний радиус сердечника,
R = 32,5 мм; r – внутренний радиус сердечника, r = 19,5 мм.

Средняя длина магнитопровода определяется по формуле

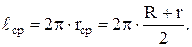
Ферритовый сердечник с обмоткой помещается в электропечь. Концы обмотки катушки подключаются к входным клеммам цифрового измерителя индуктивности AM-3003. В печь помещается датчик цифрового измерителя температуры DT-838. Включается печь, и через каждые 5−10 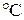прибором измеряется индуктивность. Печь нагревается до тех пор, пока не будет полной потери магнитных свойств феррита. По экспериментальным данным рассчитывается зависимость m = f(t) по формуле (7.2). По зависимости m = f(t) вычисляются значения ТК_m и строится зависимость ТК_m = f (t).

Для определения точки Кюри на спаде зависимости m = f(t) проводится касательная к наиболее крутой части спада m и точка Кюри определяется как точка пересечения касательной с осью температур (рис. 7.1).

В дальнейшем эту работу решили перевести на ЭВМ по следующим причинам:

1) занятия на заочном отделении пропускает очень много студентов и провести ее потом с каждым студентом не удается, поэтому они теперь смогут выполнить работу дома на компьютере, а стенд посмотреть на фотографии;

2) для правильного определения точки Кюри необходимо успеть снять несколько точек на падающей части зависимости L = f(t) (рис. 7.3).

Рис. 7.3. Зависимость L = f(t)

Процесс нагрева катушки длится обычно 30–35 мин., а процесс падения
L − всего 30–40 с. Если не успли снять эти точки, то печь надо остудить и нагрев повторить. Зависимость каждый раз новая. Студенты обычно лишь
с 2–3 раза могли «поймать» необходимое количество точек на спаде. Поэтому было решено один раз тщательно снять зависимость L = f(t), а потом на основе этих данных создать программу на ЭВМ и растянуть во времени на ней спад индуктивности.

Использование программы вместо экспериментальной установки имеет ряд преимуществ:

1) время спада увеличено примерно в 4 раза, и теперь большинство студентов успевают снять зависимость с первого раза;

2) теперь катушку за время лабораторной работы можно успеть нагреть несколько раз, так как не надо ждать, пока остынет печь;

3) зависимость L = f(t) не меняется от нагрева к нагреву;

4) лабораторная работа на экране монитора организована примерно так же, как и на реальной установке, а познакомиться с экспериментальной установкой можно в лаборатории;

5) компьютер позволяет обработать полученные результаты и построить на экране монитора все зависимости, которые раньше строились вручную;

6) компьютер позволяет точнее определить точку Кюри;

7) программа оценивает правильность выполнения работы (работа считается выполненной, если не было допущено ни одной ошибки).

На рисунке 7.4 приведено изображение экспериментальной установки на экране монитора.

Рис. 7.4. Изображение установки на экране монитора

Порядок выполнения работы на ЭВМ

1. Включить ЭВМ и загрузить программу лаб7.exe.

2. Ввести номер варианта задачи, указанный преподавателем, и списать параметры катушки.

3. Внимательно прочитать все тексты, выводимые на экран.

4. Выполнить I этап работы (нагревание катушки с ферритовым сердечником марки 3000 НМ):

– познакомиться с экспериментальной установкой на экране монитора;

– подготовить таблицу для заполнения (табл. 7.1)

Таблица 7.1

– выбрать режим нагрева печи так, чтобы успевать измерять индуктивность катушки, причем температура печи изменяется непрерывно, запись следует делать тогда, когда значение температуры выводится синим цветом;

– включить печь и успеть измерить индуктивность катушки для 53 фиксированных значений температуры, результаты занести в таблицу 7.1 (если не удалось записать несколько значений, то необходимо повторить нагрев с другой скоростью);

– построить зависимость L = f(t) (рис. 7.5) (зависимость будет выведена на экран только в случае, если безошибочно будут введены восемь значений
L и t, выбранные из таблицы с помощью генератора случайных величин);

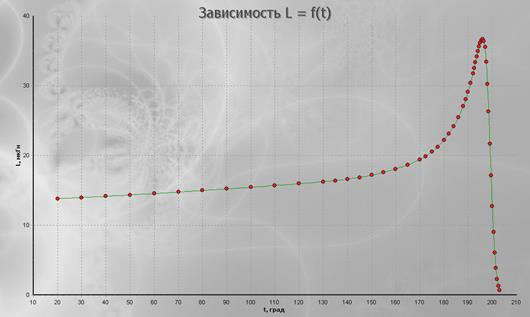
Рис. 7.5. Зависимость L = f(t)

– оценить результаты I этапа.

5. Выполнить II этап работы (построение зависимостей m = f(t) и ТК_m = f(t), определение точки Кюри):

– определить начальную магнитную проницаемость катушки m;

– рассчитать зависимость m = f(t), результаты занести в таблицу 7.1, по ней построить график (зависимость будет выведена на экран только в случае, если безошибочно будут введены 3 значения m, выбранные из таблицы с помощью генератора случаных величин);

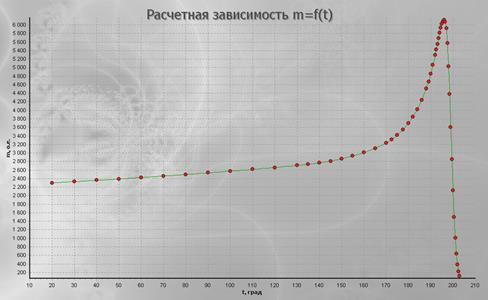
Рис. 7.6. Зависимость m = f(t)

– рассчитать зависимость ТК_m = f(t), результаты занести в таблицу 7.1, по ней построить график (зависимость будет выведена на экран только в случае, если безошибочно будут введены 3 значения ТК_m, выбранные из таблицы с помощью генератора случайных величин);

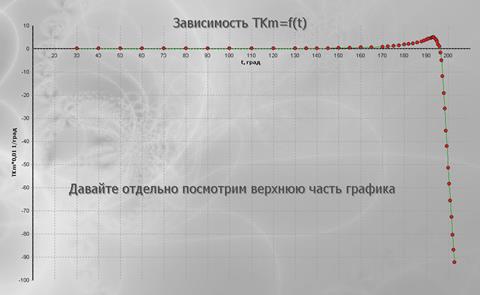
Рис. 7.7. Зависимость ТК_m = f(t)

– определить точку Кюри с помощью ЭВМ (для этого нужно растянуть зону падения m на весь экран, провести несколько касательных через каждые две соседние точки графика на спаде и выбрать из них ту, у которой получается наибольший наклон, т.е. наибольшее по модулю значение производной 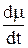(рис. 7.8));

Рис. 7.8. Определение точки Кюри на ЭВМ

– оценить результаты II этапа.

6. Составить отчет, который должен содержать:

а) название работы и ее цель;

б) исходные данные;

в) основные расчетные формулы;

г) таблицу и графики L = f(t), m = (t) и ТК_m = f(t);

д) определение точки Кюри;

е) вывод.

Вопросы к защите лабораторной работы № 7

1. Что такое ферриты?

2. Назовите основные отличия ферритов от электротехнической стали.

3. Точка Кюри. Как ее определяли в лабораторной работе?

4. Какой вид имеют зависимости m = f (t) и ТК_m = f(t)?

5. Как определить относительную магнитную проницаемость m?

6. Что такое температурный коэффициент ТК_m?

7. Какой вид имеют зависимость m = f (H), В = f (H)? Нарисовать их на одном графике.

8. Какой состав имеют магнитомягкие и магнитотвердые ферриты?

9. Приведите основные характеристики магнитомягких и магнитотвердых ферритов.

10. Где применяются ферриты?