Описание установки. Аналогичная работа проводится на стенде в лаборатории (см

Аналогичная работа проводится на стенде в лаборатории (см. часть 1,
рис. 4.3). На стенде определяются основные электрические характеристики манганина и нихрома. Сначала нужно построить зависимости R = f(t). Их снимают при нагреве катушек из манганина и нихрома в печи от 20 до 300 °С.

Обе зависимости R = f(t) строятся одновременно. Это позволяет уменьшить время выполнения лабораторной работы, так как теперь не надо ждать, пока остынет печь. А потом по экспериментальным данным выполняются расчеты и строятся зависимости TK_R = f(t), r = f(t).

В этой работе используется новый стенд, отказываться от проведения этой работы нет причин. Выполнять же точно такую же работу на ЭВМ нецелесообразно, поэтому в лабораторной работе на компьютере введены существенные отличия. Здесь определяются основные электрические характеристики только манганина, но в более широком диапазоне изменения температур. И строится больше зависимостей.

Изображение катушки из манганина на экране монитора приведено на рисунке 4.3, параметры катушки зависят от варианта.

Рис. 4.3. Параметры катушки из манганина

Зависимость R = f(t) строится в два этапа. На первом этапе ее снимают при нагреве катушки из манганина в печи (рис. 4.3) от 20 до 300 °С, а на втором – при охлаждении в морозильной камере от 20 до –110 °С (рис. 4.4).

Рис. 4.4. Изображение на экране монитора испытательной установки
для нагрева

Рис. 4.5. Изображение на экране монитора испытательной установки

для охлаждения

По окончании эксперимента (в конце второго этапа) при безошибочном вводе результатов вся зависимость R = f(t) появляется на экране монитора (рис. 4.6).

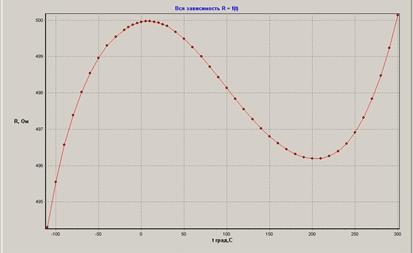
Рис. 4.6. Зависимость R = f(t) на экране монитора

По зависимости R = f(t) необходимо вычислить температурный коэффициент сопротивления:

TK_R = ∙ » ∙ ,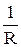

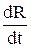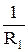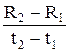где TK_R – температурный коэффициент сопротивления, 1/ 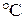; R₂ – сопротивление катушки при температуре t₂; R₁ – сопротивление катушки при температуре t₁ (t₂ > t₁ ).

Удельное сопротивление манганина определяется по формуле

r = ,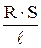

где r – удельное сопротивление в Ом×м; S – площадь сечения проводника, м²; 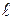– длина проводника катушки, м.

Удельное сопротивление сплава при нагревании изменяется по двум причинам:

1) с ростом температуры увеличивается амплитуда тепловых колебаний атомов, у электронов на пути возникает больше препятствий, уменьшается средняя длина свободного пробега электрона и, как следствие, растет удельное сопротивление (этот процесс характеризуется температурным коэффициентом сопротивления TK_R);

2) с ростом температуры проводник расширяется, в результате уменьшается его плотность, что приводит к дополнительному увеличению удельного сопротивления (этот процесс характеризуется температурным коэффициентом линейного расширения ).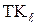

Поэтому температурный коэффициент удельного сопротивления TKr равен их сумме TKr = TK_R + 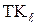. У чистых металлов TKr >> 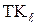, поэтому принимают TKr » TK_R. Однако у сплавов такое недопустимо.

Если удельное сопротивление манганина определить по формуле

r = ,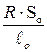

где 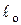– длина проводника при начальной температуре to = 20 °C; S_о – площадь сечения проводника при начальной температуре t_o, то будет учтен только температурный коэффициент сопротивления TK_R.

Поэтому при вычислении удельного сопротивления манганина необходимо учитывать также изменение линейных размеров проводника. В лабораторной работе такие измерения не проводятся, поэтому учтем изменение линейных размеров приблизительно. Будем считать, что расширение манганина происходит равномерно во всем диапазоне температур с постоянным температурным коэффициентом 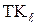» 1,8·10^-5 1/ 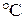. Тогда соответствующее значение удельного сопротивления можно определить по приближенной формуле

r_ℓ ,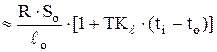

где t_i – температура, при которой вычисляется удельное сопротивление; t_o – начальная температура (t_o = 20 °C).

Расчетные зависимости r_ℓ = f(t) и r = f(t) для сравнения приведены на одном графике (рис. 4.7).

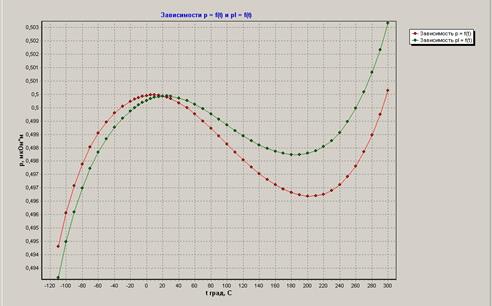
Рис. 4.7. Расчетные зависимости r_ℓ = f(t) и r = f(t)

По зависимости r_ℓ = f(t) определяется кривая TKr = f(t). Полученные зависимости TKr = f(t) и TK_R = f(t) для сравнения также нужно привести на одном графике (рис. 4.8).

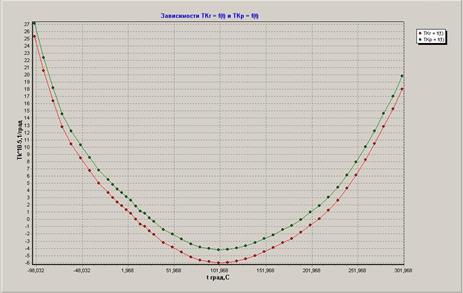
Рис. 4.8. Расчетные зависимости TKr = f(t) и TK_R = f(t)