Дзета функция.
Определение. Дзета функция Римана (Эйлера) – это сумма ряда: 
Утверждение. 1) Ряд 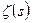 сходится равномерно внутри полуплоскости
сходится равномерно внутри полуплоскости 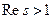 .
.
2) Функция 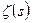 голоморфна в этой полуплоскости.
голоморфна в этой полуплоскости.
Доказательство. 1) Запишем  . Напишем:
. Напишем: 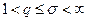 . Теперь:
. Теперь: 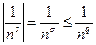 сходится т.к. q > 1. Тогда по признаку сравнения получаем наше утверждение:
сходится т.к. q > 1. Тогда по признаку сравнения получаем наше утверждение: 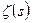 сходится равномерно для
сходится равномерно для 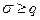 .
.
2) Следует из 1ой теоремы Вейерштрасса. 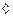
Лемма. Справедлива формула: 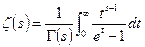 при условии, что
при условии, что 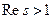 .
.
Доказательство. 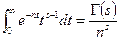 - по определению гамма функции, поэтому:
- по определению гамма функции, поэтому: 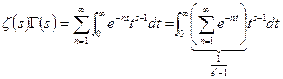 по теореме Б Леви и по теореме Лебега мы имеем право перейти к пределу под знаком интеграла.
по теореме Б Леви и по теореме Лебега мы имеем право перейти к пределу под знаком интеграла. 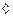
Дата добавления: 2015-09-02; просмотров: 783;
