Гамма функция.
Определение. Гамма функция (или интегралом Эйлера 2ого рода) – это следующий несобственный интеграл, зависящий от параметра: 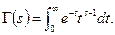
Утверждение. 1)Интеграл 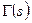 сходится равномерно внутри правой полуплоскости
сходится равномерно внутри правой полуплоскости 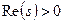 .
.
2)Функция 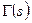 голоморфна в
голоморфна в 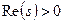 .
.
Доказательство. 1) Запишем: 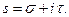 Возьмём числа:
Возьмём числа: 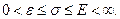 Пусть
Пусть 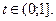 Тогда
Тогда 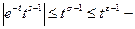 функция интегрируема на интервале (0,1)
функция интегрируема на интервале (0,1) 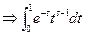 сходится равномерно для
сходится равномерно для 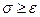 Пусть
Пусть 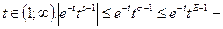 интеграл
интеграл 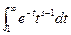 сходится равномерно на
сходится равномерно на 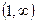 при
при 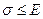 .
. 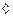
2) Следует из 1ой теоремы Вейерштрасса. 
Лемма. Справедлива формула приведения: 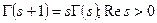 .
.
Доказательство. 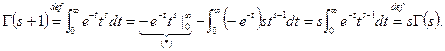 (*) = 0 т.к. на бесконечности всех убивает exp, а в 0 в силу условия
(*) = 0 т.к. на бесконечности всех убивает exp, а в 0 в силу условия 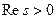 .
. 
Следствие. 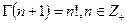 .
.
Доказательство. По индукции из леммы.
Теорема. Гамма функция аналитически продолжается на всю комплексную плоскость за исключением точек 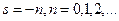 которые являются её простыми полюсами. При этом вычет функции
которые являются её простыми полюсами. При этом вычет функции 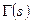 -
- 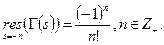
Доказательство. 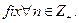 Из леммы по индукции
Из леммы по индукции 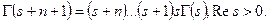 Перепишем эту формулу:
Перепишем эту формулу: 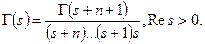 А где эта функция голоморфна на самом деле? В
А где эта функция голоморфна на самом деле? В 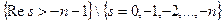 - полюсы первого порядка. Аналитическое продолжение доказано. Осталось только вычеты посчитать:
- полюсы первого порядка. Аналитическое продолжение доказано. Осталось только вычеты посчитать: 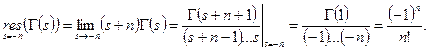
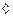
Следствие. Мах и Мin всё ближе и ближе приближаются к оси Ох со стремлением 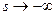 .
.
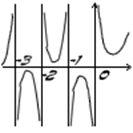
Задача. Доказать формулу дополнения: 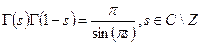 .
.
Дата добавления: 2015-09-02; просмотров: 1326;
