Функция Жуковского.

Определение. Функцией Жуковского называется 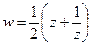(рациональная функция 2ого порядка).

Она осуществляет непрерывное отображение: 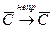. В каких точках отображение конформно? 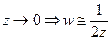- конформное отображение. 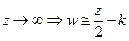т.е. в 0 и 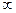отображение конформно. Рассмотрим остальные точки: 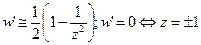здесь конформность нарушается.

Вывод. Функция Жуковского конформна в 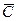, за исключением точек .

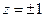Найдём области однолистности функции (биективности). Это любая область, не содержащая одновременно точек 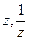. Почему? С одной стороны они переходят в 2 точки, с другой это биекция, следовательно, такого не может быть.

Пример однолистности области. А) Единичный круг. .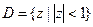

Б) Верхняя полуплоскость. 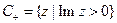. Почему? Рассмотрим инверсию.

Задача. Функция Жуковского 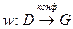? Найти эту область.

Решение. Рассмотрим расслоение единичного круга на окружности радиуса r.

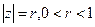
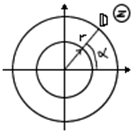
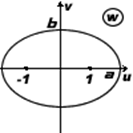
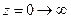, куда переходит окружность? Уравнение окружности: 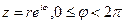, вычислим: 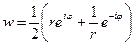. . 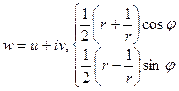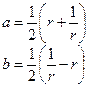- полуоси. Найдём фокусное расстояние: 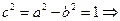Фокусы находятся в точках 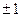. Предельные случаи такие:

Пусть 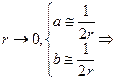почти окрестность большого радиуса. 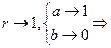область стягивается к отрезку. 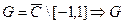искомая область, т.е. доказано.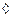

Теорема. Функция Жуковского осуществляет конформное отображение 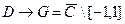единичного круга на область G, равную 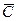с разрезом .

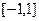Хотим выразить z через w (функцией Жуковского). 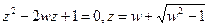- функция, обратная функции Жуковского. Знак выбрали так, чтобы z лежало в единичном круге (помним, что ).

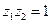Задача. Куда функция Жуковского отображает верхнюю полуплоскость?