III. Экстраполяция по темпу роста.
Возможны два варианта экстраполяции по темпу роста.
Вариант А. Прогнозное значение определяется по формуле:
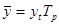 , (2.26)
, (2.26)
где 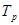 - темп роста, который находится из выражения:
- темп роста, который находится из выражения:
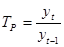 , (2.27)
, (2.27)
Вариант Б. Если имеется динамика за ряд предшествующих периодов, то можно использовать усредненный темп роста:
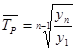 , (2.28)
, (2.28)
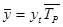 . (2.29)
. (2.29)
IV. Аппроксимация динамического ряда аналитическими функциями – расчет параметров (а, b, с) для конкретной функциональной зависимости. Параметры модели тренда должны минимизировать отклонения расчетных значений от соответствующих значений исходного ряда. Выбор модели осуществляется с помощью специально разработанных программ. Есть программы, предусматривающие возможность моделирования экономических рядов по 16-ти функциям: линейной (y = а + b * х), гиперболической различных типов (у = а + b / х), экспоненциальной, степенной, логарифмической и др. Каждая из них может иметь свою, специфическую область применения при прогнозировании экономических явлений.
Так, линейная функция применяется для описания процессов, равномерно развивающихся во времени. Параметр b (коэффициент регрессии) показывает скорость изменения прогнозируемого у при изменении х. Гиперболы хорошо описывают процессы, характеризующиеся насыщением, когда существует фактор, сдерживающий рост прогнозируемого показателя.
Модель выбирается, во-первых, визуально, на основе сопоставления вида кривой, ее специфических свойств и качественной характеристики тенденции экономического явления; во-вторых, исходя из значения критерия. В качестве критерия чаще всего используется сумма квадратов отклонений – из совокупности функций выбирается та, которой соответствует ее минимальное значение.
Для окончательного выбора вида функции нужно исследовать логику протекания процесса в целом, в том числе гипотезы его протекания в перспективе. Игнорирование этого этапа приводит к ошибочным, а иногда к парадоксальным выводам. Вы должны ответить на следующие вопросы:
· является ли исследуемый показатель величиной монотонно возрастающей, монотонно убывающей, стабильной или периодической;
· ограничен ли сверху или снизу исследуемый показатель каким-либо пределом;
· имеет ли функция, определяющая процесс, точку перегиба;
· обладает ли функция, описывающая процесс, свойством симметричности;
· имеет ли процесс четкое ограничение развития во времени?
Если в ходе предварительной обработки информации и содержательного анализа выявлено отсутствие инерционности в развитии объекта, то использование прогнозной экстраполяции недопустимо!
Выбор функции, применяемой для описания явления, зависит от типа динамики процесса. Далее будут приведены основные элементарные функции прогнозной экстраполяции.
Прогноз предполагает продление тенденции прошлого, выражаемой выбранной функцией, в будущее, т.е. экстраполяцию динамического ряда. Программным путем на ЭВМ определяется значение прогнозируемого показателя. Для этого в формулу, описывающую процесс, подставляется величина периода, на который необходимо получить прогноз.
В связи с тем, что этот метод исходит из инерционности экономических явлений и предпосылок, что общие условия, определяющие развитие в прошлом, не претерпят существенных изменений в будущем, его целесообразно использовать при разработке краткосрочных прогнозов обязательно в сочетании с методами экспертных оценок. Причем динамический ряд может строиться на основании данных не по годам, а по месяцам, кварталам.
При аппроксимации динамического ряда известными аналитическими функциями предполагается, что для прогнозирования будет использована функция, у которой форма кривой ближе всего подходит к графическому тренду. Самый простой способ выбора функции – визуальный, на основе графического изображения динамического ряда. Чаще всего для аппроксимации используются:
- линейная функция 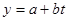 ;
;
- парабола 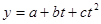 ;
;
- гипербола 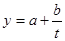 ;
;
- логарифмическая функция 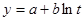 ;
;
- экспоненциальная функция 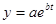 ;
;
- степенная функция 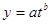 .
.
- показательная 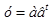 .
.
Каждая функция имеет свою сферу применения. Например, линейная функция используется для описания равномерно развивающихся процессов, а гипербола хорошо описывает процессы, для которых характерно насыщение рынка.
Для определения значений эмпирических коэффициентов 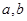 и
и 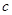 обычно используется метод наименьших квадратов. Суть данного метода заключается в определении таких значений эмпирических коэффициентов, которые минимизируют сумму квадратов отклонений расчётных и фактических значений динамического ряда:
обычно используется метод наименьших квадратов. Суть данного метода заключается в определении таких значений эмпирических коэффициентов, которые минимизируют сумму квадратов отклонений расчётных и фактических значений динамического ряда:
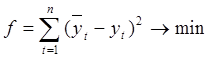 , (2.30)
, (2.30)
где 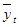 и
и 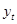 - расчетные и фактические значения;
- расчетные и фактические значения;
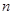 - число наблюдений.
- число наблюдений.
Так для линейной функции имеем:
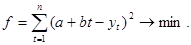 (2.31)
(2.31)
Известно, что функция имеет экстремум, если её производная равна нулю. Дифференцируя функцию по искомым переменным и приравнивая производную нулю, получаем систему линейных уравнений, решая которую найдем неизвестные эмпирические коэффициенты:
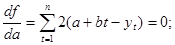 или
или 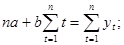 (2.32)
(2.32)
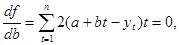
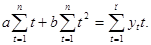 (2.33)
(2.33)
При прогнозировании исследуемого процесса в аналитическую зависимость подставляют вместо параметра 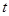 порядковый номер следующего прогнозного периода и получают точечное значение прогнозируемого параметра. Так как прогнозируемые процессы носят вероятностный характер, то помимо точечного прогноза, как правило, определяют границы возможного изменения прогнозируемого показателя – доверительные интервалы. Ширину доверительного интервала рассчитывают по формуле:
порядковый номер следующего прогнозного периода и получают точечное значение прогнозируемого параметра. Так как прогнозируемые процессы носят вероятностный характер, то помимо точечного прогноза, как правило, определяют границы возможного изменения прогнозируемого показателя – доверительные интервалы. Ширину доверительного интервала рассчитывают по формуле:
 , (2.34)
, (2.34)
где 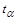 - коэффициент доверия по распределению Стьюдента, выбирается в соответствии с принятым уровнем доверительной вероятности (табл. 2.4);
- коэффициент доверия по распределению Стьюдента, выбирается в соответствии с принятым уровнем доверительной вероятности (табл. 2.4);
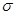 - среднеквадратическое отклонение от тренда,
- среднеквадратическое отклонение от тренда,
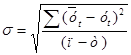 ; (2.35)
; (2.35)
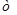 - число параметров аналитической зависимости.
- число параметров аналитической зависимости.
Таблица 2.4
Значения коэффициента доверия по распределению Стьюдента
Уровень доверительной вероятности, 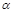
| 0,683 | 0,95 | 0,99 | 0,997 |
Коэффициент доверия, 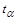
| 1,96 | 2,576 |
Для параболы 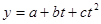 система уравнений, решая которую необходимо определить коэффициенты
система уравнений, решая которую необходимо определить коэффициенты 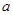 ,
, 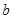 и
и 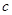 , имеет вид:
, имеет вид:
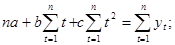 (2.36)
(2.36)
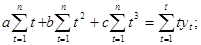
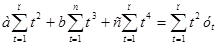 .
.
Дата добавления: 2015-09-18; просмотров: 1734;
