Нормальный закон распределения на плоскости.

На практике часто встречаются двумерные случайные величины, совместное распределение которых нормально.

Определение 1. Случайная величина 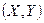называется распределенной по двумерному нормальному закону, если плотность совместного распределения есть

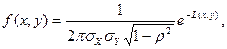(1)

где

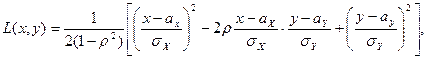
Таким образом, нормальный закон распределения на плоскости определяется пятью параметрами: 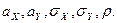Вероятностный смысл этих параметров раскрыт в следующей теореме.

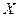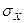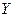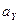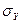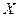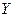Теорема 1. Составляющая имеет нормальное распределение с параметрами и . Составляющая имеем нормальное распределение с параметрами и . Коэффициент корреляции составляющих и равен .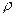

Теорема 2. Составляющие 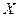и 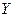независимы тогда и только тогда, когда они не коррелированны.