Зависимые и независимые случайные величины.

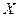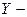Пусть и непрерывные случайные величины, допускающие непрерывное совместное распределение 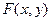с плотностью 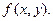Мы говорим, что случайные величины 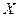и 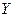независимы, если закон распределения одной из них не зависит от того, какое значение приняла другая:

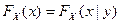; (1)

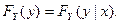(2)

Теорема 1. 1) Случайные величины 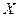и 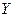независимы тогда и только тогда, когда

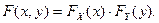(3)

2)Случайные величины 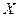и 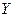независимы тогда и только тогда, когда

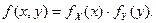(4)

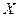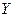Доказательство. Допустим, что и независимы. Тогда имеет место равенство (1). Это означает, что

.

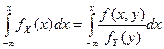
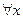Дифференцируя по 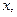получаем, что 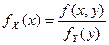, или

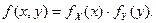
Таким образом, необходимость (4) доказана. Но тогда

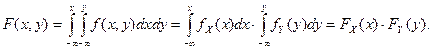
Таким образом, необходимость (3) доказана.

Обратно, пусть имеет место (3). Тогда

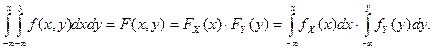
Дифференцируя последовательно по 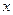и 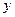, получаем (4) , откуда

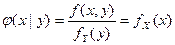, (5)

и тем самым 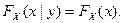Таким образом, мы доказали достаточность как (3), так и (4).

Замечание 1. Как следует из доказательства, (1) влечет за собой (2),а (2)-(1).