Значение при различных форматах стеганосообщения
| № ЦИ | Формат СС | |||
| TIF | JPEG | |||
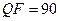
| 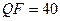
| 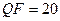
| ||
| 0.996 | 0.991 | 0.991 | 0.990 | |
| 0.946 | 0.931 | 0.928 | 0.926 | |
| 0.804 | 0.803 | 0.797 | 0.796 |
Замечание. Система (9.1) может оказаться плохо обусловленной (вырожденной) для некоторых блоков ЦИ-контейнера, что приводит к возникновению артефактов на ЦИ-стеганосообщении (рис.9.5). Как правило, это блоки, отвечающие фоновым областям изображения, перепад значений яркости пикселей в их пределах очень незначительный. Такие блоки не используются для погружения дополнительной информации. Как показывает вычислительный эксперимент, количество таких блоков в пределах изображения невелико, и их игнорирование при стеганопреобразовании не приводит к значимому снижению скрытой пропускной способности.

а

б
Рис.9.5. Пример нарушения надежности восприятия СС, формируемого стеганоалгоритмом 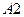 : ЦИ-контейнер (формат TIF) (а); СС (формат TIF) (б)
: ЦИ-контейнер (формат TIF) (а); СС (формат TIF) (б)
Замечание. Вычислительная сложность стеганоалгоритма 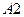 определяется количеством блоков, получаемых при стандартном разбиении
определяется количеством блоков, получаемых при стандартном разбиении 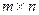 -матрицы
-матрицы 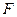 основного сообщения:
основного сообщения: 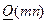 , а в случае квадратной матрицы -
, а в случае квадратной матрицы - 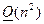 .
.
Повышение скрытой пропускной способности стеганографических алгоритмов, устойчивых к атаке сжатием.Недостатком обоих разработанных в предыдущих подразделах стеганоалгоритмов является их малая скрытая пропускная способность (СПС) —  бит/пиксель.
бит/пиксель.
Пусть 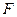 —
—  -матрица ЦИ-контейнера. В качестве дополнительной информации как и прежде рассматривается случайно сформированная бинарная последовательность
-матрица ЦИ-контейнера. В качестве дополнительной информации как и прежде рассматривается случайно сформированная бинарная последовательность 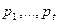 ,
, 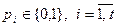 ,
, 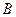 — произвольный
— произвольный 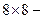 блок матрицы контейнера, полученный после ее стандартного разбиения. Матрице
блок матрицы контейнера, полученный после ее стандартного разбиения. Матрице 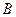 поставим в соответствии две симметричные матрицы по правилу (5.2) – (5.3):
поставим в соответствии две симметричные матрицы по правилу (5.2) – (5.3):
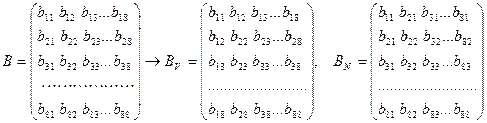 , (9.2)
, (9.2)
которые и будем рассматривать ниже как блоки контейнера. Для каждого из полученных виртуальных блоков в силу их симметричности возможно построение нормального спектрального разложения:
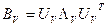 ,
, 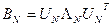 , (9.3)
, (9.3)
где 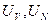 — матрицы ортонормированных лексикографически положительных собственных векторов (СВ),
— матрицы ортонормированных лексикографически положительных собственных векторов (СВ),
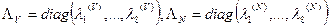 (9.4)
(9.4)
— матрицы собственных значений (СЗ) 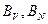 соответственно.
соответственно.
В соответствии с теоремой Фробениуса матрицы 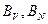 (неразложимые неотрицательные) имеют положительные СЗ
(неразложимые неотрицательные) имеют положительные СЗ 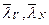 , являющиеся простыми корнями соответствующих матрицам
, являющиеся простыми корнями соответствующих матрицам 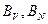 характеристических уравнений. Модули всех других СЗ
характеристических уравнений. Модули всех других СЗ 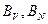 не превосходят
не превосходят 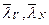 . Собственным значениям
. Собственным значениям 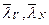 соответствуют СВ
соответствуют СВ 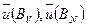 с положительными координатами. Для определенности предположим, что для (9.4)
с положительными координатами. Для определенности предположим, что для (9.4) 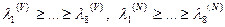 , т.е.
, т.е. 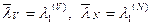 . Соответствующие этим СЗ собственные векторы —
. Соответствующие этим СЗ собственные векторы — 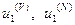 .
.
Обозначим 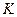 — пороговое значение вариации возмущений максимальных СЗ блоков. Учитывая связь между СНЧ и СЗ симметричной матрицы,
— пороговое значение вариации возмущений максимальных СЗ блоков. Учитывая связь между СНЧ и СЗ симметричной матрицы, 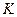 берется равным 200 для собственных значений, как и для СНЧ несимметричных блоков в СА
берется равным 200 для собственных значений, как и для СНЧ несимметричных блоков в СА 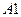 .
.
Основные шаги предлагаемого стеганоалгоритма, называемого далее 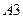 , следующие.
, следующие.
Погружение ДИ.
Шаг 1. Матрица 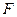 контейнера разбивается стандартным образом на блоки
контейнера разбивается стандартным образом на блоки 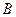 размером
размером 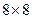 . Каждый блок используется для погружения 3 бит ДИ.
. Каждый блок используется для погружения 3 бит ДИ.
Шаг 2. (Погружение ДИ). Пусть 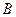 — очередной блок, используемый для стеганопреобразования,
— очередной блок, используемый для стеганопреобразования, 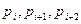 — очередные 3 бита ДИ, погружаемые в
— очередные 3 бита ДИ, погружаемые в 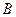 .
.
2.1. Каждому блоку 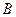 ставятся в соответствии симметричные блоки
ставятся в соответствии симметричные блоки 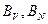 по правилу (9.2).
по правилу (9.2).
2.2. Строятся нормальные спектральные разложения (9.3) для 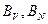 ;
;
2.3. Если 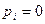 ,
,
то
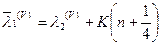 ,
,
где 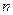 — натуральное число здесь и ниже;
— натуральное число здесь и ниже;
иначе
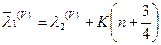 .
.
2.4. Если 
то
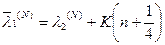 ;
;
иначе
 .
.
2.5. Если 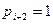 ,
,
то
2.5.1.  ,
,
где 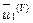 — возмущенный в ходе СП
— возмущенный в ходе СП 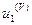
2.5.2. Приведение СВ 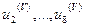 блока
блока 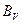 к ортонормированному с
к ортонормированному с 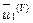 лексикографически положительному виду. Результат —
лексикографически положительному виду. Результат — 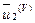 ,...,
,..., 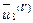 .
.
иначе
2.5.1. 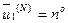 ,
,
где 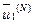 — возмущенный в ходе СП
— возмущенный в ходе СП 
2.5.2. Приведение СВ  блока
блока 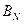 к ортонормированному с
к ортонормированному с 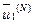 лексикографически положительному виду. Результат —
лексикографически положительному виду. Результат — 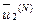 ,...,
,..., 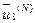 .
.
Шаг 3. (Формирование блока СС).
3.1.Если 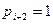 ,
,
то
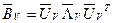 ,
, 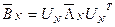 ,
,
где 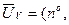
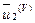 ,...,
,..., 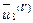 ),
), 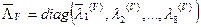 ,
, 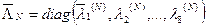
иначе
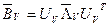 ,
, 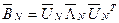 ,
,
где 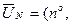
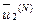 ,...,
,..., 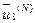 ),
), 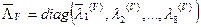 ,
, 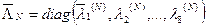 .
.
3.2. Элементы матриц 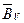 и
и 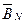 обозначим соответственно
обозначим соответственно 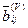 ,
,  .
.
Блок 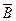 СС будет иметь вид:
СС будет иметь вид:
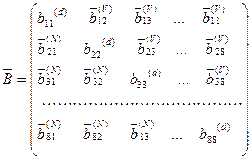 . (9.5)
. (9.5)
Вычисление элементов 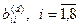 , стоящих на главной диагонали
, стоящих на главной диагонали 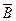 , обсуждается ниже.
, обсуждается ниже.
Декодирование ДИ.
Шаг 1. Матрица 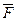 СС разбивается стандартным образом на блоки
СС разбивается стандартным образом на блоки 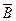 размером
размером 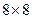 . Каждый блок используется для декодирования 3 бит ДИ.
. Каждый блок используется для декодирования 3 бит ДИ.
Шаг 2. (Декодирование ДИ). Пусть 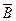 — очередной блок, из которого извлекаются биты
— очередной блок, из которого извлекаются биты 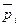 ,
, 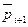 ,
, 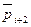 ДИ.
ДИ.
2.1. Каждому блоку ставятся в соответствии симметричные блоки 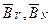 по правилу (9.2).
по правилу (9.2).
2.2. Строятся нормальные спектральные разложения вида (9.3):
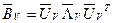 ,
, 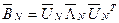 .
.
2.3. Если 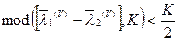 , где
, где 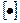 — целая часть аргумента
— целая часть аргумента
то 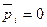 ;
;
иначе 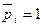 .
.
2.4. Если 
то 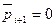 ;
;
иначе 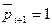 .
.
2.5.Найти 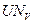 и
и 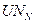 — углы между векторами
— углы между векторами 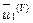 и
и 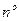 ,
, 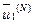 и
и 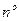 соответственно.
соответственно.
Если 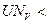
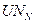 ,
,
то 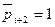 ,
,
иначе  .
.
Для вычисления диагональных элементов в (3.6) рассматривались варианты: способ 1 – диагональ 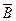 совпадает с диагональю
совпадает с диагональю 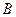 ; способ 2 – элементы диагонали
; способ 2 – элементы диагонали 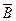 равны среднему арифметическому между соответствующими элементами
равны среднему арифметическому между соответствующими элементами 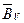 и
и 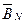 ; способ 3 – диагональ
; способ 3 – диагональ 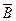 совпадает с диагональю
совпадает с диагональю 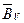 , если при погружении ДИ
, если при погружении ДИ 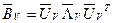 (т.е. погружается
(т.е. погружается 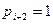 ), с диагональю
), с диагональю 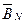 , если при погружении
, если при погружении 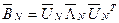 (погружается
(погружается 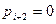 ).
).
Для выбора способа получения диагональных элементов 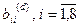 , блока
, блока 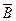 стеганосообщения был проведен вычислительный эксперимент, где были задействованы 400 ЦИ из базы NRCS (по 200 изображений в форматах JPEG, TIF), которая традиционно используется для тестирования стеганографических алгоритмов. Атака сжатием моделировалась путем сохранения стеганосообщения в формат JPEG с различными коэффициентами качества
стеганосообщения был проведен вычислительный эксперимент, где были задействованы 400 ЦИ из базы NRCS (по 200 изображений в форматах JPEG, TIF), которая традиционно используется для тестирования стеганографических алгоритмов. Атака сжатием моделировалась путем сохранения стеганосообщения в формат JPEG с различными коэффициентами качества 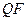 . Результаты эксперимента представлены в таблице 9.4.
. Результаты эксперимента представлены в таблице 9.4.
Таблица 9.4
Зависимость 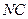 от значения коэффициента качества
от значения коэффициента качества 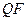 , используемого при атаке сжатием на СС, при различных способах определения диагональных элементов блока СС в алгоритме
, используемого при атаке сжатием на СС, при различных способах определения диагональных элементов блока СС в алгоритме 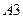
| Формат хранения ЦИ-контейнера | Способ получения диагональных элементов 
| Среднее значение 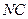 при различных значениях коэффициента качества при различных значениях коэффициента качества 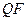 , используемого при сжатии СС , используемого при сжатии СС
| |||
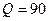
| 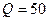
| 
| 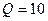
| ||
| TIF | 0.8957 | 0.8733 | 0.8602 | 0.8466 | |
| 0.8891 | 0.8611 | 0.8358 | 0.8350 | ||
| 0.9400 | 0.9359 | 0.9325 | 0.9079 | ||
| JPEG | 0.8814 | 0.8726 | 0.8562 | 0.8396 | |
| 0.8769 | 0.8437 | 0.8415 | 0.8301 | ||
| 0.9398 | 0.9357 | 0.9279 | 0.9109 |
Из результатов вычислительного эксперимента вытекает:
· при формировании блока СС целесообразно для вычисления элементов главной диагонали использовать способ 3;
· наибольшее возмущение погруженная ДИ получает в процессе формирования СС (накопление вычислительной погрешности), а не в процессе последующего сжатия;
· эффективность 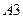 не зависит от формата используемого контейнера.
не зависит от формата используемого контейнера.
Сравнение эффективности стеганоалгоритмов 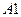 ,
, 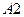 ,
, 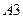 (способ 3) для контейнеров в формате TIF, представлены на рис.9.6.
(способ 3) для контейнеров в формате TIF, представлены на рис.9.6.
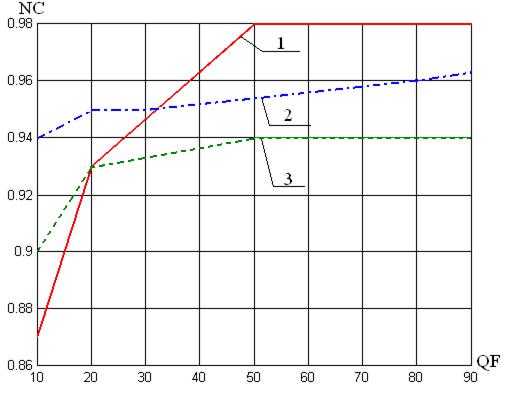
Рис.9.6. Эффективность декодирования ДИ разработанными стеганоалгоритмами: 1 ― 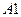 ; 2 ―
; 2 ― 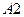 ; 3 ―
; 3 ― 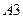
Из результатов эксперимента видно, что эффективности, оцениваемые как устойчивость к атаке сжатием, всех трех разработанных стеганоалгоритмов являются достаточно высокими и сравнимыми между собой. И хотя 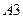 несколько уступает
несколько уступает 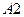 и
и 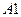 для
для  , это ухудшение является предсказуемым (в
, это ухудшение является предсказуемым (в 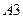 вычислительная погрешность очевидно окажется больше при формировании стеганосообщения, чем в
вычислительная погрешность очевидно окажется больше при формировании стеганосообщения, чем в 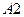 и
и 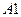 ) и незначительным, но СПС для
) и незначительным, но СПС для 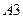 в три раза больше, чем для
в три раза больше, чем для 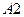 и
и 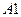 , и составляет
, и составляет 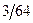 бит/пиксель.
бит/пиксель.
Замечание. Вычислительная сложность СА 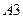 определяется количеством блоков, получаемых при стандартном разбиении
определяется количеством блоков, получаемых при стандартном разбиении 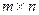 -матрицы
-матрицы 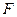 контейнера:
контейнера: 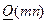 , а в случае квадратной матрицы —
, а в случае квадратной матрицы — 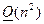 .
.
Дата добавления: 2015-09-18; просмотров: 1028;
