УМНОЖЕНИЕ И ДЕЛЕНИЕ ЧИСЛА НА ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ УГЛОВ
а) Умножение числа на синус и косинус угла:
a = b·sina; d = b·cosa.
Порядок решения (шкалы 3 и 5):
— передвигая движок, установить индекс у против деления шкалы 5, соответствующего числу (рис. 16 и 17);
— установить визирку по шкале 4 (если заданный угол меньше 5° или больше 175°) или по шкале 3 (если заданный угол больше 5° или меньше 175°) на деление, соответствующее заданному углу;
— отсчитать по визирке на шкале 5 искомое произведение.
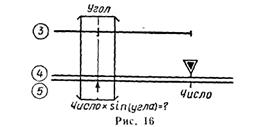
Примечание. Для умножения числа на значение косинуса угла необходимо устанавливать визирку на деление шкалы 3 или 4, соответствующее дополнению угла до 90°, т. е. (90° — α).
Пример.Дано: b — 325; а — 28°.
Находим: α = 325 sin 28° = 152; d = 325 cos 28° = 325 sin 62° = 286.
б) Умножение числа на тангенс и котангенс угла
α = b tgα; d = b·ctg α.
Порядок решения (шкалы 4и 5):
— передвигая движок, установить индекс  против деления шкалы 5, соответствующего заданному числу (рис. 17);
против деления шкалы 5, соответствующего заданному числу (рис. 17);
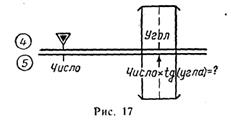
— установить визирку по шкале 4 на деление, соответствующее заданному углу;
— отсчитать по визирке на шкале 5 искомое произведение.
Примечание. Для умножения чисел на котангенс угла необходимо устанавливать визирку по шкале 4 на деление, соответствующее дополнению угла до 90°, т. е. (90° — α).
Пример.Дано: b = 15,4; а = 58°.
Находим: а = 15,4 tg 58° = 24,6; d = 15,4 ctg 58° = 15,4 tg 32° = 9,62.
в) Деление числа на синус и тангенс угла
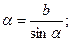
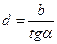
Порядок решения (шкалы 3 и 5):
— установить визирку по шкале 5 на деление, соответствующее заданному числу (рис. 18 и 19);
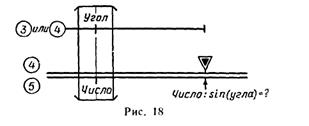
— передвигая движок, подвести под визирку деление шкалы 4 (если число делится на тангенс или заданный угол меньше 5° или больше 175°) или шкалы 3 (если число делится на синус и заданный угол больше 5° или меньше 175°), соответствующее заданному углу;
— отсчитать по шкале 5 против индекса  искомое частное.
искомое частное.
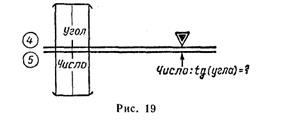
Примечания: 1. При делении чисел на косинус угла необходимо подводить под визирку деления шкалы 3 или 4, соответствующие дополнению угла до 90°, т. е. (90° — α).
Пример. Дано: b = 123; а = 36°.
Находим: 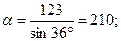
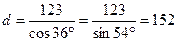
2. Величины тангенса и котангенса угла являются взаимообратными. Поэтому деление на эти величины целесообразно заменить умножением, а именно:
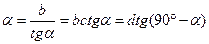
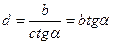
Порядок решения таких выражений описан выше.
Примеры:
1) 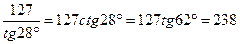
2) 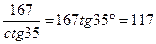
3. При умножении или делении чисел на значения секансов или косекансов углов целесообразно заменить умножение чисел на значения секансов или косекансов углов делением чисел на значения косинусов или синусов этих углов, а деление заменить умножением и выполнять указанные действия так же, как описано выше.
Примеры: 1) 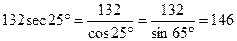 .
.
2) 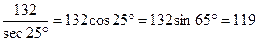 .
.
3) 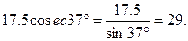 .
.
4) 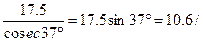 .
.
Дата добавления: 2015-09-18; просмотров: 4291;
