ПРОДУКЦИИ И СИСТЕМЫ ПОСТА

ПРОДУКЦИОННЫЕ СИСТЕМЫ

Рассмотрим еще одну формальную модель, в которой уточняется понятие алгоритма и вычислимой функции. Такая модель имеет разнообразные практические приложения и отличается от модели рекурсивных функций по способам представления алгоритмов и механизму их выполнения, но функционально эквивалентна ей. Эта формализация лежит в основе современного логического программирования и моделей алгоритмов символьной обработки.

ПРОДУКЦИИ И СИСТЕМЫ ПОСТА

Пусть А, Bи V -три непересекающихся конечных алфавита, причем А È B ¹Æ, которые называются соответственно основным алфавитом, вспомогательным алфавитом и алфавитом переменных.

В дальнейшем всегда будет предполагаться, что |АÈB| ³ 2.

Всякое слово, составленное из символов алфавитов А, B и V, называется образцом.

Слово 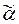Î(A È B)* называется применением образцаt, если существует подстановка Q= 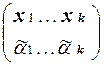, где x₁, . . . , x_k - все различные символы переменных, входящих в t, а 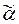₁, . . . , 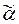_k- непустые слова в алфавите А 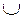B, что слово 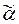получается изtзаменой каждого вхождения символов переменных x₁, . . . , x_k на соответствующие им слова в подстановке Q.

Применение подстановки Q к образцу t обозначается как tQ.

Всякий образец представляет собой структурное описание множества всех своих применений, т.е. множества слов, строение которых задается образцом.

Например, если A = {0, 1}, B = 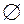, V = {x}, то образец t = 1x0 представляет все правильные записи не менее чем трехразрядных четных двоичных чисел. Образец x1x представляет двоичные последовательности, составленные из двух одинаковых последовательностей разделенных 1.

Различные образцы соответствуют различным классам слов, структура которых описывается этими образцами. Такое свойство следует из следующего утверждения.