Глава 2. Философия и методология синергетики

§ 1. Феномен синергетики

Термин «синергетика» был впервые использован в начале 70-х годов 20 века немецким физиком Германом Хакеном. Происходит это слово от греческого «synergeia» - совместное действие, сотрудничество. Сегодня под синергетикой понимают междисциплинарную науку о самоорганизации – спонтанном (естественном) возникновении порядка из хаоса. Основными источниками появления и развития синергетики были термодинамика и новый раздел математики, получивший название «теория катастроф», основоположником которого считается французский математик Ренэ Том. В развитии идей новых направлений термодинамики, получивших название «неравновесной термодинамики», большой вклад внесли такие ученые, как норвежский физико-химик Ларс Онсагер и бельгийский физик русского происхождения Илья Пригожин.

§ 2. Синергетика и термодинамика

Одним из основных «корней», из которых произрастает синергетика, является термодинамика – наука о тепловых процессах. В составе современной термодинамики выделяют более ранние и классические разделы, получившие название «равновесная термодинамика», и более поздние и неклассические ее разделы, называемые обычно «неравновесной термодинамикой». Рассмотрим вкратце основные идеи этих направлений термодинамики для лучшего понимания того, что представляет из себя синергетика.

В равновесной термодинамике основным является понятие термодинамического равновесия, т.е. такого состояния термодинамической системы, при котором она не обменивается материей и энергией с окружающей средой (такая система называется изолированной) и не меняется во времени (такая система называется стационарной). Равновесная термодинамика базируется на трех основных законах. 1-й закон – это закон сохранения энергии, 2-й закон – закон неубывания энтропии в изолированной системе, и 3-й закон – закон недостижимости абсолютного нуля температур.

В неравновесной термодинамике рассматриваются процессы, в той или иной мере отклоняющиеся от термодинамического равновесия. В линейной неравновесной термодинамике такое отклонение еще невелико, что выражается в так называемом принципе локального равновесия, при котором термодинамическое равновесие сохраняется в достаточно малых частях системы. В этом случае термодинамические процессы могут быть описаны в форме линейных зависимостей присутствующих в системе потоков вещества или энергии от различных термодинамических сил, вызывающих эти потоки. Например, поток тепла вызывается силой, определяемой перепадом температур, поток вещества – перепадом концентраций в системе, и т.д. В работах Онсагера и Пригожина была сформулирована идея некоторой величины, получившей название «производство энтропии», к минимизации которой стремится стационарная термодинамическая система в случае небольших отклонений от состояния равновесия. Производство энтропии – это величина скорости изменения энтропии, так что стационарная система стремится минимизировать скорость изменения энтропии, максимально приближаясь в этом к состоянию термодинамического равновесия, когда производство энтропии равно нулю. Более того, стационарное состояние с минимумом производства энтропии оказывается термодинамически устойчивым состоянием, т.е. происходит погашение малых отклонений (флуктуаций), удаляющих систему от этого состояния.

В нелинейной неравновесной термодинамике отклонение от состояния равновесия может быть достаточно значительным. Здесь уже нельзя пользоваться линейными соотношениями между потоками и силами, перестает выполняться принцип локального равновесия. Неравновесие присуще не только системе в целом, оно проникает и на уровень малых частей системы. Тем не менее, было обнаружено, что как раз в такого рода далеко отстоящих от равновесия состояниях спонтанно возникают различные упорядоченные структуры, которые способны поддерживать свое состояние только в высоконеравновесных условиях. Такие структуры были названы «диссипативными структурами»: это «структуры в открытых системах, в которых в ходе неравновесного процесса из пространственно-однородного состояния самопроизвольно (спонтанно) возникает пространственная или временная структура»[25]. В таких системах обычно локально энтропия уменьшается, хотя глобально считается, что она по-прежнему растет.

В нелинейной неравновесной термодинамике существует ряд типичных примеров возникновения и существования диссипативных структур. Это:

1) переход ламинарного («спокойного») течения жидкости в турбулентное («вихревое»). Хотя внешне кажется, что турбулентное движение представляет из себя потерю всякой упорядоченности, на деле оказывается, что здесь обнаруживается более сложный порядок.

2) возникновение «ячеек Бернара». Если поставить на огонь сковородку с налитым в нее минеральным маслом, то при определенной температуре в масле возникнут красивые гексагональные ячейки, вызванные конвенцией масла между более горячим и менее плотным нижним слоем и более холодным и плотным верхним слоем масла.

3) возникновение когерентного излучения в лазере, когда, после первоначального хаотического излучения и начиная с некоторой мощности накачки, атомы вещества начинают излучать фотоны одной фазы, что выражается в возникновении мощного пучка лазерного излучения.

4) реакция Белоусова-Жаботинского, выражающаяся в красивой пространственной организации химических реакций, которая особенно заметна при окрашивании среды в различные цвета, в зависимости от состава реагирующих компонентов.

5) модель «хищник - жертва», описывающая периодические процессы зависящих друг от друга численностей популяций двух биологических видов, один из которых выступает как хищник, другой – как его жертва. Нарастание численности хищников приводит к последующему падению численности жертвы, что затем сказывается в падении численности хищника, что впоследствии позволяет размножиться жертве, что, в свою очередь, влечет увеличение численности хищника, который уменьшает численность жертвы…, и так далее, процесс начинает циклично повторяться.

На последнем примере мы видим, что нелинейная неравновесная термодинамика начинает порождать некоторые общие методы рассмотрения процессов самоорганизации, которые выходят за границы только тепловых процессов. Еще более ясно это видно в математическом аппарате синергетики – теории катастроф.

§ 3. Синергетика и теория особенностей

Математический аппарат синергетики предполагает описание различных систем – физических, биологических, экономических. Для этого синергетике нужен достаточно универсальный язык. Одно из основных понятий такого языка – понятие «фазовое пространство» или «пространство состояний» системы. В общем случае, при изучении самых различных систем может оказаться, что состояние системы возможно описать некоторым набором параметров, или «степеней свободы». Например, чтобы описать механическую систему из N точек, нужно описать положение каждой точки в пространстве и ее скорость. Положения и скорости – это вектора в трехмерном пространстве, и каждый такой вектор представляет из себя три числа в некоторой системе координат. Следовательно, на каждую точку придется три числа вектора положения и три числа вектора скорости – всего 6 чисел. Для описания N точек потребуется в этом случае 6N чисел. Каждое из этих чисел будет степенью свободы системы в 6N-мерном фазовом пространстве. Чтобы описать систему «хищник-жертва», достаточно две степени свободы – численность популяции хищника и численность популяции жертвы. Итак, первое, что необходимо отметить: синергетика работает с некоторыми абстрактными пространствами, каждая точка которых – это не обязательно положение в пространстве, но общее состояние системы. В качестве координат в таких пространствах выступают некоторые степени свободы, параметры, на основе которых может быть однозначно описано каждое состояние системы. Такое пространство мы далее будем называть «пространством состояний» системы.

Хотя пространства состояний не обязательно являются геометрическими пространствами (например, они могут иметь число измерений более трех), но эти пространства можно пытаться изучать так, словно они являются геометрическими пространствами. Например, обычно та или иная синергетическая система может принимать не все возможные состояния в пространстве состояний, но только лишь некоторую их часть. Это связано с наложением каких-либо ограничений, например, законов или правил, на возможное поведение системы. Обычно такие части пространств, в которых система может принимать свои состояния, называют «поверхностями», по аналогии с геометрическими поверхностями. Система в этом случае принимает свои состояния, находящиеся только на поверхности. Она может быть представлена как точка, движущаяся по поверхности. В этом случае обычно оказывается, что все параметры системы можно разделить на два класса – управляющие и управляемые. Управляющие параметры системы – это такие ее параметры, которые можно менять независимо от остальных параметров, через них можно как бы управлять поведением всей системы в целом, в то время как управляемые параметры оказываются зависимыми от управляющих параметров, меняются вслед за их изменением таким образом, чтобы состояние системы всегда находилось на соответствующей поверхности.

В связи с этим оказалось, что теория поверхностей в абстрактных многомерных пространствах тесно связана с описанием поведения различных систем в синергетике. Первые фундаментальные результаты в этой области были получены американским математиком Хасслером Уитни, который развил так называемую «теорию особенностей». Давайте коснемся вначале понятия «особенности» в этом подходе, а затем свяжем это понятие с идеями синергетики.

Представим себе трехмерное пространство с координатами XYZ, в котором расположена двумерная сфера. Построим проекцию этой сферы на координатную плоскость XY (см. рис.3).

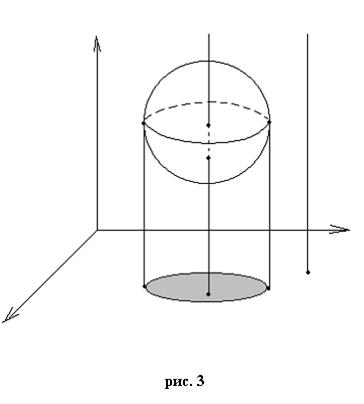
Мы видим, что все точки на плоскости проецирования XY можно разбить на три класса, в зависимости от того, сколько прообразов имеют эти точки на сфере. Точки вне круга имеют 0 прообразов. Точки на границе круга – 1 прообраз (эти прообразы лежат на «экваторе» сферы). Наконец, точки внутри круга имеют по два прообраза – один на нижней, второй – на верхней полусфере. В этом случае особенностью под названием «складка Уитни» будет являться то множество точек на сфере, проекции которых на плоскости проецирования XY разделяют области точек с разным числом прообразов. В данном случае это будет «экватор» сферы. Именно его проекция на плоскость XY образует окружность, разделяющую области с нулевым и двойным числом прообразов на сфере.

Еще одним примером широко распространенной особенности является так называемая «сборка Уитни» (рис.4). В этом случае на поверхности образуется область изогнутой деформации, передне-верхний и задне-нижний край которой как раз образуют особенность, разделяющую множества точек на плоскости проецирования с одним и тремя прообразами (в проекции самой особенности лежат точки с двумя прообразами).

Какое же отношение имеет теория особенностей к синергетике ?

Дело в том, что самое интересное и сложное в поведении синергетической системы – это наличие разного рода скачков, или «катастроф», когда система, при непрерывном изменении управляющих параметров резко и скачком меняет значение управляемых параметров. Оказалось, что такого рода катастрофы удается описывать как процессы пересечения особенностей на поверхности состояний системы. В этом случае управляющие параметры принадлежат плоскости проецирования поверхности, а управляемые параметры испытывают «бифуркацию» (раздвоение или размножение), выбирая из множества прообразов на поверхности один из нескольких прообразов.

Рассмотрим этот процесс на примере так называемой «машины катастроф» немецкого математика Зимана. Это довольно простое устройство (см. рис.5), представляющее из себя плоскую дощечку с закрепленным в ее правой части вращающимся диском. Через гвоздик и край диска натянута резинка с карандашом, который может рисовать на левой части дощечки. Передвигая карандаш, мы будем заставлять вращаться тем или иным образом диск. Таким образом, состояние этой системы описывается положением карандаша и диска. Положение карандаша – это две координаты (x,y) его кончика в левой части доски.

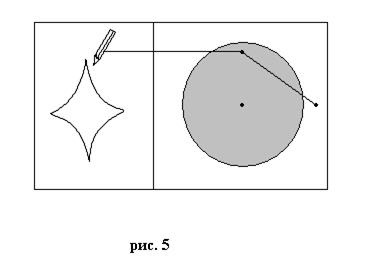
Положение диска можно описать через угол отклонения j от линии, соединяющей гвоздик и центр диска. В целом состояние системы описывается здесь как точка (x,y,j) трехмерного пространства состояний системы. Положение карандаша (x,y) представляет из себя систему управляющих параметров, а положение диска j - управляемый параметр. Меняя положение карандаша, мы тем самым меняем положение диска, причем диск в этом случае принимает не какие угодно положения, но какие-то определенные. Следовательно, изменение системы может быть описано в этом случае как движение по некоторой поверхности в трехмерном пространстве состояний системы. Самое интересное в этом случае состоит в том, что если карандаш непрерывно подводить к некоторой кривой в левой части дощечки, то, при пересечении этой кривой, будет происходить резкий скачок («катастрофа») диска из одного положения в другое. Оказалось, что такая кривая, которая назвается «кривой катастроф», представляет из себя проекцию на плоскость сборки Уитни, так что изменение системы в случае машины катастроф может быть представлено как перемещение по поверхности состояний, имеющей особенность в виде сборки Уитни. Хотя сама поверхность геометрически не видна, и представляет из себя поверхность в абстрактном пространстве состояний системы, но проекция особенности этой поверхности может быть наглядно изображена в виде кривой катастроф в левой части дощечки. Невидимое обнаруживает себя в видимом.

§ 4. Сводка основных понятий синергетики

Математика синергетики имеет дело с различными фазовыми пространствами, эволюция динамической системы в которых обычно описывается той или иной системой дифференциальных уравнений. Эволюционный процесс может быть изображен как траектория в фазовом пространстве (фазовая кривая), производная этой кривой представляет из себя фазовую скорость. В этом случае положением равновесия системы называется точка фазового пространства, в котором фазовая скорость равна нулю. Положения равновесия могут быть устойчивыми или неустойчивыми, в зависимости от того, будут ли компенсироваться со временем небольшие отклонения системы от положения равновесия. Графическое представление фазовых траекторий вблизи положений равновесия носит название фазового портрета.

В фазовом пространстве могут существовать такие множества точек, к которым со временем стремятся фазовые траектории. Такие множества точек называются аттракторами. В качестве аттракторов могут выступать устойчивые состояния равновесия или, например, предельные циклы – замкнутые кривые в фазовом пространстве, попав на которые, точка начинает как бы вращаться по этим кривым. Внешне такие вращения выражаются в разного рода колебаниях параметров системы, например, в колебаниях численности популяций хищника и жертвы. Особо выделяются так называемые странные аттракторы. Они представляют из себя множество точек со сложной геометрией, попав в которое, фазовая кривая навсегда остается в этом множестве, но очень сложно ведет себя в нем. Геометрия странных аттракторов является фрактальной. Фракталами называют такие математические структуры, которые обычно обладают свойствами самоподобия и дробной размерности. Классическим примером фрактальной структуры является так называемая кривая Коха (рис.6).

На рисунке изображены последовательные этапы ее построения: мы начинает с равностороннего треугольника, затем на каждой из его сторон достраиваем малые треугольники, на их сторонах – еще меньшие треугольники, и так далее, до бесконечности. Кривой Коха называется то, что получится при оставлении только внешнего контура фигуры (рис. 7).

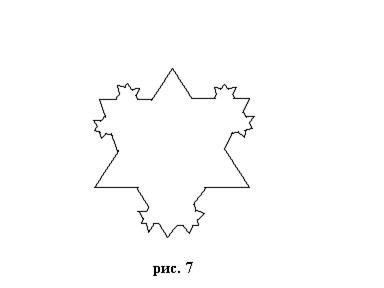
и в бесконечном пределе такого построения.

Наглядно представить себе такую «кривую» конечно невозможно. Замечательно также и то, что размерность этой кривой больше единицы, но меньше, чем два. Это и не одномерная кривая, и не двумерная поверхность. Это нечто среднее, напоминающее может быть «уплотненную кривую» или «продырявленную поверхность». Кроме того, если мы увеличим под микроскопом любой участок кривой Коха, то он обнаружит тот же «рисунок», что и первоначальный участок – так наглядно в этом примере проявляет себя самоподобие, т.е. подобие частей целому, во фрактальных структурах.

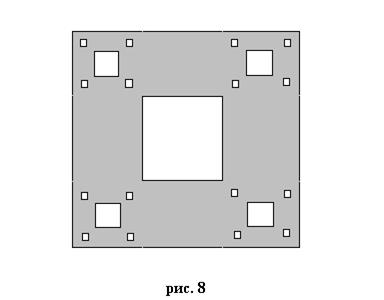
Еще один наглядный пример фрактала – так называемый ковер Серпинского. На рисунке 8 показан один из этапов его построения.

Мы начинаем с квадратного участка плоскости, затем вырезаем в нем центральный квадрат. В получившихся угловых малых квадратных участках также вырезаем центральные малые квадраты, и так повторяем до бесконечности, бесконечно «продырявливая» первоначальный кусок. В пределе получается «бесконечно-дырявая плоскость», которая уже не является плоскостью, но в то же время еще не становится линией. Это и есть ковер Серпинского, названный так в честь польского математика Серпинского, и вновь обладающий промежуточной – между единицей и двумя – размерностью.

Странные аттракторы представляют из себя фрактальные структуры. Попадая в них, фазовая кривая начинает сложно блуждать, со временем бесконечно близко подходя к любой точки фрактала, и в то же время две разные фазовые кривые очень быстро расходятся внутри странного аттрактора, даже если вначале они были близки. Из-за последнего свойства резко затруднены предсказания точного поведения фазовой кривой внутри странного аттрактора – небольшие отклонения от известной траектории здесь могут повести к непредсказуемым особенностям поведения внутри аттрактора. Именно с этим связаны, например, трудности предсказания погоды в современной метеорологии.

Поведение фазовой кривой в странном аттракторе хотя и весьма непредсказуемо, но тем не менее это поведение отличается от просто случайного, например, от броуновского движения молекул. Дело в том, что случайное поведение системы не может быть в точности воспроизведено во второй раз, в то время как поведение фазовой кривой даже внутри странного аттрактора в точности воспроизводимо при тех же начальных условиях. Чтобы выделить поведение системы внутри странного аттрактора и отличать его от просто случайных блужданий, используется такой специальный термин, как детерминированный хаос. Это и есть тип поведения фазовой кривой в странном аттракторе.

Часть фазовой кривой до ее попадания в аттрактор может быть названа нестационарным поведением динамической системы. Внутри аттрактора фазовая кривая выражает стационарное поведение системы.

Часто эволюция динамической системы описывается не просто дифференциальным уравнением, но уравнением, в которое входит некоторый характеристический параметр. Для каждого частного значения такого параметра будет получаться свое дифференциальное уравнение, а значит и своя структура решений этого уравнения. Для множества структур решений, зависящих от параметра, можно ввести понятие режима функционирования динамической системы – как такого множества решений уравнения, которые качественно не отличаются друг от друга. В рамках одного режима функционирования изменение параметра уравнения приводит к непрерывному изменению структуры решения уравнения. Каждому режиму функционирования присуща своя структура решения со своими аттракторами. Переход от одного режима функционирования к другому при непрерывном изменении характеристического параметра называется бифуркацией, что буквально означает «удвоение», так как классическим примером смены режимов стали случаи удвоения положений равновесия. Значение характеристического параметра, при котором происходит бифуркация, называется точкой бифуркации. Здесь наблюдается прямая аналогия с теорией особенностей, как она была описана выше, когда происходит скачкообразное изменение управляемых параметров при непрерывном изменении управляющих параметров системы. Следует только иметь в виду, что выше мы использовали теорию особенностей для описания структуры фазового пространства в рамках одного режима функционирования, в то время как понятие «бифуркация» предполагает как бы «теорию особенностей второго порядка», когда рассматриваются переходы между разными режимами функционирования динамической системы.

При переходе от одного режима функционирования к другому происходит потеря устойчивости старых аттракторов и возникает устойчивость аттракторов нового режима функционирования.

Бифуркации можно разделить на «мягкие» и «жесткие». Мягкие бифуркации характеризуются небольшим отличием режимов функционирования, например, достаточной близостью новых аттракторов по отношению к старым. Жесткие бифуркации, которые после работ французского математика Рене Тома в начале 70-х годов стали называть «катастрофами», характеризуются значительным отличием старого и нового режимов функционирования, например, значительным удалением новых аттракторов от старых в фазовом пространстве системы. В этом случае качественный скачок в изменении поведения системы может быть особенно значительным – «катастрофическим». В работах Рене Тома все катастрофы были сведены к 7 элементарным, которые носят следующие интересные названия: складка, сборка, ласточкин хвост, бабочка, гиперболическая омбилика, эллиптическая и параболическая омбилика.

§ 5. Обобщенный образ синергетической системы

Синергетическая система

- есть открытая система, как правило находящаяся в состоянии, далеком от термодинамического равновесия

- обладает высокой степенью чувствительности к влияниям внешней среды, т.к. находится в состоянии неустойчивого фазового равновесия и способна выйти из этого состояния под действием малых отклонений (флуктуаций)

- из всех флуктуаций системой фиксируется наиболее оптимальная и невероятная (с точки зрения термодинамического равновесия) флуктуация, способная привести к новому режиму функционирования системы

- новый режим функционирования проявляет себя в виде новой диссипативной структуры, которая постепенно распространяется из некоторой локальной области («ядра»). Этот процесс носит название нуклеации

- нуклеация распространяется, части системы обнаруживают кооперативность, и наконец скачком (катастрофически) возникает новая упорядоченная структура

- новая структура выражает максимальную адаптацию системы к изменившимся условиям среды, представленным как управляющие параметры системы или характеристические параметры ее динамики (описывающих эту динамику дифференциальных уравнений)

Здесь мы видим следующие корреляции: по мере удаления от равновесия повышается чувствительность системы к внешней среде, возникает своего рода различимость системы по отношению к нужным флуктуациям, которые отбираются и усиливаются в форме разного рода когерентных (кооперативных) эффектов.

Такой образ синергетической системы уже во многом напоминает образ живого организма, также далекого от равновесия, чувствительного к среде, обладающего избирательной различимостью и способного к формированию системной активности.

В лице равновесной и неравновесной термодинамики (синергетики) современная наука выражает идею своего рода двух состояний материи. Материя может находиться в более инертном, равновесном состоянии, описываемой средствами равновесной термодинамики, и материя способна достигать некоторого «возбужденного», или «активированного», состояния, выражаемого средствами неравновесной нелинейной термодинамики и синергетики. Причем, в активированном состоянии материя начинает до некоторой степени напоминать состояние живого организма. Методология синергетики начинает во многом напоминать своего рода «обобщенный дарвинизм», оперирующий понятиями «изменчивости», «отбора» и «адаптации» на универсальном уровне синергетических обобщений, выходящих далеко за границы только биологического знания. Такого рода тенденцию изменения представлений о материи в современной физике можно было бы условно обозначить термином «витализация образа материи», от латинского vita – жизнь, т.е. как бы «оживление» представлений о материи, сближающее ее с образом живого организма.

Синергетику сопровождают сегодня и разного рода современные версии более идеалистических философских систем. Можно говорить об элементах платонизма, проявляющегося в утверждении некоторых первичных форм (элементарных катастроф), определяющих активность материальных процессов, о возрождении до некоторой степени идей дальнодействия, связанного с разного рода нелокальными, мгновенными взаимодействиями в процессе образования кооперативных структур. Образ витализированной материи в синергетике близок также философии стоиков, которая рассматривала мир как бесконечную иерархию самовозрастающих логосов-огней, укорененных в материи и прорастающих в ней в виде разного рода структур и активностей.

§ 6. Сильная и слабая синергетика

На фоне синергетики как строгой науки рождается сегодня некоторое новое мировоззренческое движение, использующее идеи синергетики далеко за пределами ее конкретной области приложения. Это своего рода «синергетическая парадигма», пытающаяся выразить некоторый новый образ мира в неклассической науке 20-21 века. О такой «синергетике» мы будем говорить как о «сильной синергетике», поскольку она предполагает равноправное расширение своих методов на область в том числе «сильных систем» - биологических, социальных и даже духовных. В этом случае синергетику как науку, преимущественно рассматривающую «слабые системы» - физические и химические, - можно было бы условно обозначить как «слабую синергетику».

«Слабая» синергетика обеспечена хорошо развитым математическим аппаратом, который вкратце был описан выше. В то же время попытки прямо перенести этот аппарат на процессы в человеческом сознании, искусстве, культуре обычно не удаются. Дело в том, что в этих, более гуманитарных областях, мы имеем дело с существенно субъектными онтологиями, которые обладают специфической структурностью и своим особенным логосом. Поэтому «сильная» синергетика, провозглашаемая как некоторый новый универсальный язык науки, хотя и обладает, по-видимому, большим потенциалом развития, но большинством ученых воспринимается пока с некоторой осторожностью. Скорее перенесение методов синергетики в гуманитарную область рассматривается сегодня в большей степени на уровне некоторой метафоричности. Хорошей иллюстрацией такой манеры использования языка синергетики является следующий пример английского математика К.Зимана. Предположим, что творческая личность, например ученый, может быть охарактеризована такими параметрами научного творчества, как уровень владения техникой (Т) исследований в некоторой науке, степенью увлеченности (У) и уровнем научных достижений (Д). Последний параметр во многом определяется первыми двумя, т.е. Т и У могут быть представлены как управляющие параметры, Д – как управляемый параметр в некотором трехмерном фазовом пространстве. Можно предположить, что творческая эволюция ученого может быть описана как движение по некоторой поверхности в фазовом пространстве. На основе опытных данных можно говорить о трех основных типах творческих личностей: 1) «нормальные ученые» (если использовать терминологию Т.Куна – см. ниже), отличающиеся небольшой увлеченностью. Их уровень достижений медленно возрастает по мере улучшения техники исследований. 2) ученые с высокой степенью увлеченности. Здесь Зиман выделяет два подвида: 2.1) «гении» - ученые, наряду с высокой увлеченностью, постоянно наращивающие технику исследований, что в итоге может привести к резкому скачку их научных достижений. 2.2) «маньяки» - личности, сочетающие высокую увлеченность с достаточно низкой техникой, что рано или поздно приводит их к резкому падению научных достижений.

Такого рода типологию, считает Зиман, можно было бы выразить в форме поверхности в фазовом пространстве, имеющей сборку Уитни в качестве особенности (см. рис.9).

В этом случае эволюция «нормальных ученых» может быть выражена как линия вне особенности, выражающая непрерывную зависимость Д от У и Т. При небольшом У постепенное нарастание Т приводит здесь к столь же постепенному и небольшому нарастанию Д. Траектории «гениев» и «маньяков», в силу высокой увлеченности У, попадают в зону особенности, однако движутся они здесь по-разному. «Гении», при высоком уровне У, начинают повышать Т и пересекают особенность «снизу» (от точки 1 к точке 2), что дает им возможность скачка на верхнюю часть поверхности.

«Маньяки», наоборот, все более усиливая У и оставаясь примерно на одном уровне Т, попадают в особенность «сверху» (от точки 3 к точке 4), что грозит им падением «вниз», на нижнюю часть поверхности. Хотя в некоторые промежуточные моменты эволюции «гении» и «маньяки» могут быть близки друг другу, но финалы их эволюции в этом случае качественно различны.

Хотя такого рода модели могут быть интересны, но пока их можно воспринимать лишь качественно, без возможности строгого количественного анализа. Трудности количественного анализа в этом случае носят глобальный характер, вытекающий из обсуждаемой выше проблематичности соотношения субъектности и математических структур.

Одним из проявлений философии «сильной синергетики» является также идея американского физика Фримена Дайсона о так называемой «зеленой технологии», т.е. о таком типе технологий, которые строились бы на тех же принципах, что и процессы в живой природе. Это технологии с более гибким и мягким синергетическим управлением, когда система более высокого уровня управляет только переходами системы более низкого уровня в моменты бифуркаций, в остальном же поведение подчиненной системы является автономным. «Зеленые технологии» должны будут противостоять современным «серым технологиям» с жестким централизованным управлением.