Естественный способ.

Для задания движения точки естественным способом необходимо знать траекторию точки с заданным на ней началом и положительным направлением отсчета по дуге траектории дуговой координаты (рис.2). Тогда положение точки в любой момент времени определяют дуговой координатой S, измеренной по дуге траектории от начала отсчета, и уравнение движения точки при этом способе задания движения имеет вид:

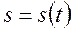
Рисунок 2

При этом способе задания движения , вводят связанную с движущейся точкой М подвижную прямоугольную систему координат Mτnb (см. рис.2) . Оси этой системы координат (оси естественного трехгранника) направлены таким образом: касательная ось Мτ – по касательной к траектории в направлении увеличения координаты S, главная нормаль Mn – перпендикулярно к касательной в сторону вогнутости траектории, бинормаль Mb – перпендикулярно первым двум осям, образуя с ними правую систему координат. Орты 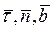этих координатах осей устанавливают известные из дифференциальной геометрии три взаимно перпендикулярные направления (касательная, главная нормаль и бинормаль) и создают координатные плоскости: соприкасающаяся плоскость проходит через касательную ось и главную нормаль, нормальная плоскость– через главную нормаль и бинормаль, а спрямляющая плоскость – через касательную и бинормаль. Если траектория точки является плоской кривой, то она размещена в соприкасающейся плоскости.

...