Теоретические упражнения.
1. Ряды 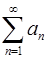 и
и 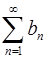 сходятся. Доказать, что ряд
сходятся. Доказать, что ряд 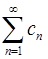 сходится, если
сходится, если 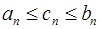 .
.
У к а з а н и е. Рассмотреть неравенства 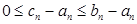 .
.
2. Ряд 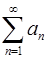
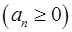 сходится. Доказать, что ряд
сходится. Доказать, что ряд 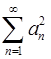 тоже сходится. Показать, что обратное утверждение неверно.
тоже сходится. Показать, что обратное утверждение неверно.
3. Ряды 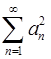 и
и 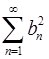 сходятся. Доказать, что ряд
сходятся. Доказать, что ряд 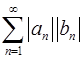 тоже сходится.
тоже сходится.
У к а з а н и е. Доказать и использовать неравенство 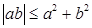 .
.
4. Ряды 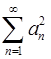 и
и 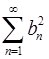 сходятся. Доказать, что ряд
сходятся. Доказать, что ряд 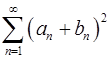 тоже сходится.
тоже сходится.
5. Пусть ряд 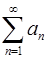 сходиться и
сходиться и 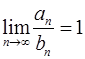 . Можно ли утверждать, что сходиться ряд
. Можно ли утверждать, что сходиться ряд 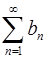 ?
?
Рассмотреть пример 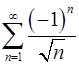 и
и 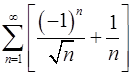 .
.
6. Пусть ряд 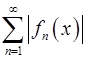 сходиться равномерно на отрезке
сходиться равномерно на отрезке 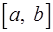 . Доказать, что ряд
. Доказать, что ряд 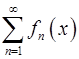 так же сходиться равномерно на этом отрезке.
так же сходиться равномерно на этом отрезке.
7. Может ли функциональный ряд на отрезке:
а) сходиться равномерно и не сходиться абсолютно,
б) сходиться абсолютно и не сходиться равномерно?
Рассмотреть примеры:
a) 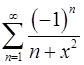 , отрезок
, отрезок 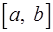 произвольный;
произвольный;
б) 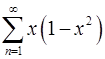 , отрезок
, отрезок 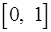 .
.
8. Показать, что функция 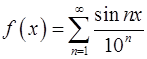 всюду непрерывна.
всюду непрерывна.
9. Доказать, что ряд 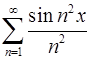 сходится равномерно в интервале
сходится равномерно в интервале 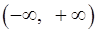 . Можно ли его дифференцировать в этом интервале?
. Можно ли его дифференцировать в этом интервале?
10. Доказать, что если ряд 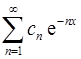 сходиться в точке
сходиться в точке 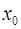 , то он сходиться абсолютно
, то он сходиться абсолютно 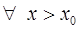 .
.
Дата добавления: 2015-09-11; просмотров: 527;
