Работа расширения. Работа в термодинамике, так же как и в механике, определяется произведени­ем действующей на рабочее тело силы на путь ее действия.

Работа в термодинамике, так же как и в механике, определяется произведени­ем действующей на рабочее тело силы на путь ее действия.

Рассмотрим газ массой М и объемом V, заключенный в эластичную оболочку с поверхностью F.

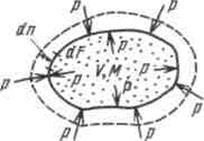Если газу сообщить некоторое количество теплоты, то он будет расширяться, совершая при этом работу против внешнего давления р, оказываемого на него средой. Газ дей­ствует на каждый элемент оболочки dF с силой, равной pdF и, перемещая ее по нормали к поверхности на расстояние dn, совершает элементарную работу pdFdn. Общую работу, совершенную в течение бесконечно малого процесса, получим, интегрируя данное выражение по всей поверхности F оболочки: .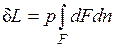

Из рисунка видно, что изменение объема dV выражается в виде интеграла по поверхности: , следовательно

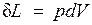. (3.1)

При конечном изменении объема работа против сил внешнего давления, называе­мая работой расширения, равна

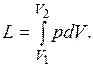
Из (3.1) следует, что 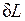и dV всегда имеют одинаковые знаки:

если dV>0, то и 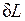>0, т. е. при расширении работа тела положительна, при этом тело само совершает работу;

если же dV<0, то и 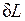<0, т. е. при сжатии работа тела отрицательна: это означает, что не тело совершает работу, а на его сжатие затрачивается работа извне. Единицей измерения работы в СИ яв­ляется джоуль (Дж).

Отнеся работу расширения к 1 кг массы рабочего тела, получим

l = L/M; .

Величина , представляющая собой удельную работу, совершаемую систе­мой, содержащей 1 кг газа, равна

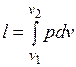. (3.2)

Поскольку в общем случае р — вели­чина переменная, то интегрирование воз­можно лишь тогда, когда известен закон изменения давления р = р(v).

Формулы (3.1) — (3.2) справедливы только для равновесных процессов, при которых давление рабочего тела равно давлению окружающей среды.

В термодинамике для исследования равновесных процессов широко исполь­зуют р,v – диаграмму, в которой осью аб­сцисс служит удельный объем, а осью ординат — давление. Поскольку состоя­ние термодинамической системы опреде­ляется двумя параметрами, то на р,v – диаграмме оно изображается точкой. На рисунке точка 1 соответствует начально­му состоянию системы, точка 2 — конеч­ному, а линия 12 — процессу расшире­ния рабочего тела от v1 до v2. При бесконечно малом изменении объема площадь заштрихованной вертикальной полоски равна 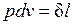; следовательно, работа процесса 12 изо­бражается площадью, ограниченной кри­вой процесса, осью абсцисс и крайними ординатами.

Таким образом, работа из­менения объема эквивалентна площади под кривой процесса в диаграмме р, v (рисунок 3.1).

Рисунок 3.1 - Графическое изображение работы в р, v – координатах

Каждому пути перехода системы из состояния / в состояние 2 (например, 12, 1а2 или 1b2) соответствует своя работа расширения.Следова­тельно, работа зависит от характера термодинамического процесса, а не явля­ется функцией только исходного и ко­нечного состояний системы. С другой стороны, зависит от пути интегри­рования и, следовательно, элементарная работа не является полным диффе­ренциалом.

Работа всегда связана с перемеще­нием макроскопических тел в простран­стве, например перемещением поршня, деформацией оболочки, поэтому она ха­рактеризует упорядоченную (макрофизическую) форму передачи энергии от од­ного тела к другому и является мерой переданной энергии. Поскольку величина пропорцио­нальна увеличению объема, то в качестве рабочих тел, предназначенных для пре­образования тепловой энергии в механи­ческую, целесообразно выбирать такие, которые обладают способностью значи­тельно увеличивать свой объем. Этим качеством обладают газы и пары жидко­стей. Поэтому, например, на тепловых электрических станциях рабочим телом служат пары воды, а в двигателях внут­реннего сгорания — газообразные про­дукты сгорания того или иного топлива.