Уравнение состояния
Для равновесной термодинамической системы существует функциональная связь между параметрами состояния, которая называется уравнением состояния. Опыт показывает, что удельный объем, температура и давление простейших систем, которыми являются газы, пары или жидкости, связаны термическим уравнением состояния вида 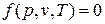 .
.
Уравнению состояния можно придать другую форму: 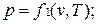
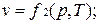
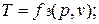
Эти уравнения показывают, что из трех основных параметров, определяющих состояние системы, независимыми являются два любых.
Для решения задач методами термодинамики совершенно необходимо знать уравнение состояния. Однако оно не может быть получено в рамках термодинамики и должно быть найдено либо экспериментально, либо методами статистической физики. Конкретный вид уравнения состояния зависит от индивидуальных свойств вещества.
Уравнение состояния идеальных газов
Из уравнений (1.1) и (1.2) следует, что 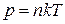 .
.
Рассмотрим 1 кг газа. Учитывая, что в нем содержится N молекул и, следовательно, 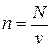 , получим:
, получим: 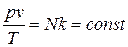 .
.
Постоянную величину Nk, отнесенную к 1 кг газа, обозначают буквой R и называют газовой постоянной. Поэтому
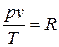 , или
, или 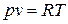 . (1.3)
. (1.3)
Полученное соотношение представляет собой уравнение Клапейрона.
Умножив (1.3) на М, получим уравнение состояния для произвольной массы газа М: 
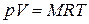 . (1.4)
. (1.4)
Уравнению Клапейрона можно придать универсальную форму, если отнести газовую постоянную к 1 кмолю газа, т. е. к количеству газа, масса которого в килограммах численно равна молекулярной массе μ. Положив в (1.4) М=μ и V=V μ, получим для одного моля уравнение Клапейрона — Менделеева:
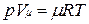 .
.
Здесь 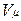 — объем киломоля газа, а
— объем киломоля газа, а 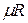 — универсальная газовая постоянная.
— универсальная газовая постоянная.
В соответствии с законом Авогадро (1811г.) объем 1 кмоля, одинаковый в одних и тех же условиях для всех идеальных газов, при нормальных физических условиях равен 22,4136 м3, поэтому
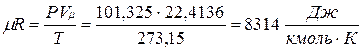
Газовая постоянная 1 кг газа составляет 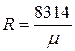 .
.
Уравнение состояния реальных газов
В реальных газах вотличие от идеальных существенны силы межмолекулярных взаимодействий (силы притяжения, когда молекулы находятся на значительном расстоянии, и силы отталкивания при достаточном сближении их друг с другом) и нельзя пренебречь собственным объемом молекул.
Наличие межмолекулярных сил отталкивания приводит к тому, что молекулы могут сближаться между собой только до некоторого минимального расстояния. Поэтому можно считать, что свободный для движения молекул объем будет равен 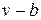 , где b — тот наименьший объем, до которого можно сжать газ. В соответствии с этим длина свободного пробега молекул уменьшается и число ударов о стенку в единицу времени, а следовательно, и давление увеличивается по сравнению с идеальным газом в отношении
, где b — тот наименьший объем, до которого можно сжать газ. В соответствии с этим длина свободного пробега молекул уменьшается и число ударов о стенку в единицу времени, а следовательно, и давление увеличивается по сравнению с идеальным газом в отношении 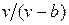 , т. е.
, т. е.
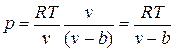 .
.
Силы притяжения действуют в том же направлении, что и внешнее давление, и приводят к возникновению молекулярного (или внутреннего) давления. Сила молекулярного притяжения каких-либо двух малых частей газа пропорциональна произведению числа молекул в каждой из этих частей, т. е. квадрату плотности, поэтому молекулярное давление обратно пропорционально квадрату удельного объема газа: рмол = а/v2, где а — коэффициент пропорциональности, зависящий от природы газа.
Отсюда получаем уравнение Ван-дер-Ваальса (1873 г.):
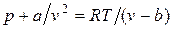 ,
,

 или
или
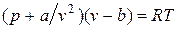 .
.
При больших удельных объемах и сравнительно невысоких давлениях реального газа уравнение Ван-дер-Ваальса практически вырождается в уравнение состояния идеального газа Клапейрона, ибо величина a/v2
(по сравнению с p) и b (по сравнению с v) становятся пренебрежимо малыми.
Уравнение Ван-дер-Ваальса с качественной стороны достаточно хорошо описывает свойства реального газа, но результаты численных расчетов не всегда согласуются с экспериментальными данными. В ряде случаев эти отклонения объясняются склонностью молекул реального газа к ассоциации в отдельные группы, состоящие из двух, трех и более молекул. Ассоциация происходит вследствие несимметричности внешнего электрического поля молекул. Образовавшиеся комплексы ведут себя как самостоятельные нестабильные частицы. При столкновениях они распадаются, затем вновь объединяются уже с другими молекулами и т. д. По мере повышения температуры концентрация комплексов с большим числом молекул быстро уменьшается, а доля одиночных молекул растет. Большую склонность к ассоциации проявляют полярные молекулы водяного пара.
Дата добавления: 2015-09-02; просмотров: 769;
