Поле бесконечной заряженной нити
 
|
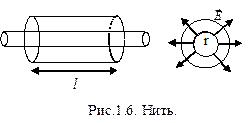
Окружим нить цилиндром длиной l и площадью поперечного сечения S. Т.к. вектор напряженности электрического поля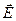 
направлен через боковую поверхность, а через две торцевые поток отсутствует, то по теореме О-Г:
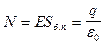, Sб. п.= l 2pr, 2p Еlr = 
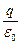Þ 
.
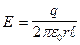Если ввести понятие линейной плотности зарядов t = q/l - заряд распределенной по всей длине, то напряженность поля нити можно определить так:
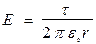. (1.28)
Напряженность поля создаваемая телом любой формы может быть получена с помощью т. О-Г.
Работа, совершаемая силами электростатического поля при малом перемещении точечного заряда в этом поле, равна убыли потенциальной энергии в рассматриваемом поле:
dА = q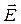 
d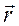 
= - dWn.
Для системы из n точечных зарядов
.
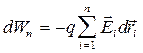После интегрирования получим:
,
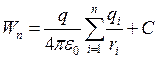где С - постоянная интегрирования.
Значение С зависит от выбора начала отсчета потенциальной энергии заряда q в электростатическом поле. Если система имеет бесконечную протяженность в пространстве, то полагают, потенциальная энергия равна нулю в точке, бесконечно удаленной от всех зарядов qi системы, т.е. С=0:
.
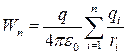Если заряды системы распределены в пространстве непрерывно, то для напряженности поля справедлива формула:
.
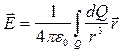Тогда потенциальная энергия в случае при вышеуказанном выборе начала отсчета потенциальной энергии
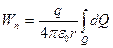. (1.29)
Из (1.29) следует, что потенциальная энергия не может служить характеристикой самого поля. Энергетической характеристикой поля служит его потенциал.
Потенциалом электростатического поля называется физическая величина, равная отношению потенциальной энергии пробного заряда, помещенного в рассматриваемую точку поля, к этому заряду:
j = Wп /q . (1.30)
Тогда, учитывая (1.29):
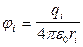или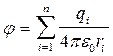 
.
Таким образом,
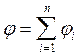, (1.31)
т.е. при наложении электростатических полей их потенциала складываются алгебраически.
Из формул (1.4) и (1.30):
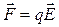, Wп = qj .
С другой стороны, существует связь:
.
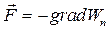Т.к. заряд q не зависит от координат точек поля, то
grad(qj)=q×gradj. (1.32)
Элементарная работа сил электростатического поля на малом перемещении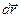 
пробного заряда q
,
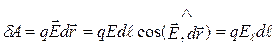где dl = |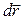 
|, El - проекция вектора 
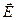на направление перемещения .
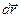С другой стороны,
δA = -dWп= -qdj.
Поэтому
El dl = -dj или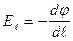 
, (1.33)
т.е. проекция вектора напряженности электростатического поля на произвольное направление численно равна быстроте убывания потенциала поля на единицу длины в этом направлении.
.
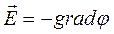Геометрическое место точек электростатического поля, в которых значения потенциала одинаковы, называется эквипотенциальной поверхностью. Если вектор 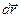направлен по касательной к эквипотенциальной поверхности, то (dj/dl) = 0 и El = 0, т.е. 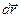^ 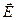. Следовательно, эквипотенциальные поверхности ортогональны линиям напряженности (рис. 1.7). Работа, совершаемая силами электростатического поля при перемещении электрического заряда по одной и той же эквипотенциальной поверхности, равна нулю.
Описание метода исследования и установки
В основе этой работы лежит метод математического моделирования. Это такое моделирование, при котором закономерности различных по природе физических явлений описываются одинаковыми дифференциальными уравнениями с граничными условиями. Тождественность математического описания позволяет заменить сложные исследования одного явления более простым исследованием другого.
Тот факт, например, что электрическое поле стационарного тока в слабопроводящей среде является потенциальным, позволяет использовать его для моделирования электростатического поля заряженных тел в вакууме.
Тождественность таких потенциальных полей математически можно обосновать следующим образом.
Для плотности тока j в электролите справедливо условие div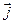 
= 0. С другой стороны 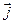= s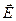 
, где s - удельная электрическая проводимость среды и 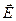=-grad 
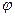, учитывая, что во всем объёме проводящей среды s = const, можно записать:
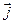= -s grad j и div 
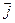= -s div grad j = -sDj = 0
-это уравнение записано для плоскости.
Таким образом, имеются две потенциальные функции (одна - в вакууме, другая - в слабопроводящей среде), которые удовлетворяют условию Dj = 0 и на границах поля принимают одинаковые значения. Из теории потенциального поля следует, что эти функции должны быть тождественны во всех точках поля. Поэтому для изучения поля электрических зарядов можно использовать поле тока в слабопроводящей среде (электропроводная бумага, раствор электролита и т.п.). При его моделировании силовым линиям электростатического поля будут соответствовать линии тока, а поверхностям равного потенциала - поверхности равных напряжений. Напряжение различных точек модели может быть измерено вольтметром, мостовым или компенсационным методом.
Для исследования распределения потенциала в стационарных электрических полях тока используют зонды, вводимые внутрь поля. Зондом является тонкий металлический стержень, хорошо изолированный по всей длине, кроме конца. Эксперимент значительно упростится, если проводить исследование плоского стационарного поля тока. Потенциалы измеряются при помощи зонда на поверхности токопроводящей бумаги. Это обыкновенная бумага с нанесенным на ее поверхность слоем сажи или графита. Такие модели включаются в электрическую цепь с помощью электродов (металлических шин). Токопроводящая бумага вместе с электродами закрепляется на специальном планшете. Стационарное электрическое поле связано с наличием электрического тока, и это упрощает измерение разности потенциалов между любыми двумя точками поля. Для этого достаточно прикоснуться к этим точкам щупами (зондами), которые подключены к вольтметру.
Таким образом, на электропроводной бумаге могут быть получены линии равного потенциала. Линии тока соответствую силовым линиям моделируемого электростатического поля. Их можно построить, начертив ортогональные кривые к экспериментально полученным линиям равного потенциала. Для того чтобы определить напряженность поля в заданной точке необходимо: измерить расстояние до нее от двух электродов Dх1 и Dх2 , знать значение потенциала в этой точке Dj. Тогда по формуле:
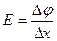, (1.34)
можно будет определить Е1 и Е2. Нахождение результирующего значения происходит по принципу суперпозиции полей.
Схема цепи
1. 
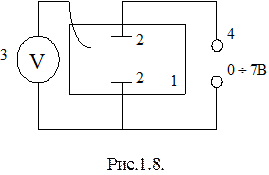1.Токопроводящая бумага.
2. Электроды.
3. Мультиметр в режиме вольтметра.
4. Источник постоянного тока 0¸7В.
Дата добавления: 2015-09-11; просмотров: 2138;