Поле бесконечной однородно заряженной плоскости

Рассмотрим как, создаваемое бесконечной плоскостью, заряженной с постоянной поверхностной плотностью s

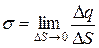. (13.11)

Рис. 13.4. Из соображений симметрии вытекает, что напряженность в любой точке поля имеет направление перпендикулярное к плоскости.

Представим себе мысленно цилиндрическую поверхность с образующими, перпендикулярными к плоскости, и основаниями величины DS, расположенными относительно плоскости симметрично. Применим к этой поверхности теорему Гаусса. Поток через боковую часть поверхности будет отсутствовать, поскольку Е_п в каждой ее точке равна нулю.

Для оснований Е_п совпадает с Е. Следовательно, суммарный поток через поверхность будет равен 2ЕDS. Внутри поверхности заключен заряд s×DS. Согласно теореме Гаусса должно выполняться условие

2ЕDS = ,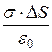

откуда Е = 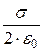. (13.12)