Основное уравнение центробежного насоса

Согласно известной из курса гидравлики одноразмерной теории движение массы жидкости в рабочем колесе может быть уподоблено движению одной элементарной струйки, т.е. движение всей массы жидкости в рабочем колесе рассматривается как движение одинаковых элементарных струек в колесе с бесконечно большим числом элементарно тонких лопаток.

При этом, кроме того, допускается, что траектории движения отдельных частиц жидкости одинаковы с формой лопаток.

Стенки проточных каналов в корпусе центробежного насоса неподвижны, поэтому скорости потока относительно этих стенок являются абсолютными скоростями.

При движении внутри канала рабочего колеса частица жидкости имеет по отношению к колесу относительную скорость w, которая направлена по касательной к лопатке в точке ее приложения. Но благодаря вращению колеса при числе оборотов п частица жидкости приобретает и окружную скорость, направленную по касательной к окружности радиуса г, определяемую как произведение угловой скорости на радиус r - расстояние рассматриваемой частицы от центра вращения, т. е.:

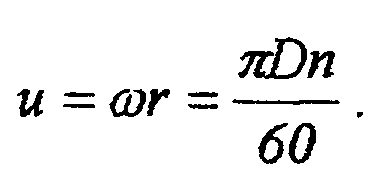
Следовательно, частица жидкости, покидая рабочее колесо, будет иметь окружную скорость по касательной к наружному диаметру колеса в точке выхода и относительную скорость, направленную по касательной к выходной кромке лопатки. В результате геометрического сложения этих скоростей (и и w) частица жидкости будет иметь абсолютную скорость с по их равнодействующей (по диагонали параллелограмма, построенного на направлениях скоростей и и м>), в направлении которой элементарные струйки жидкости будут выходить из рабочего колеса (рис. 2.2.).

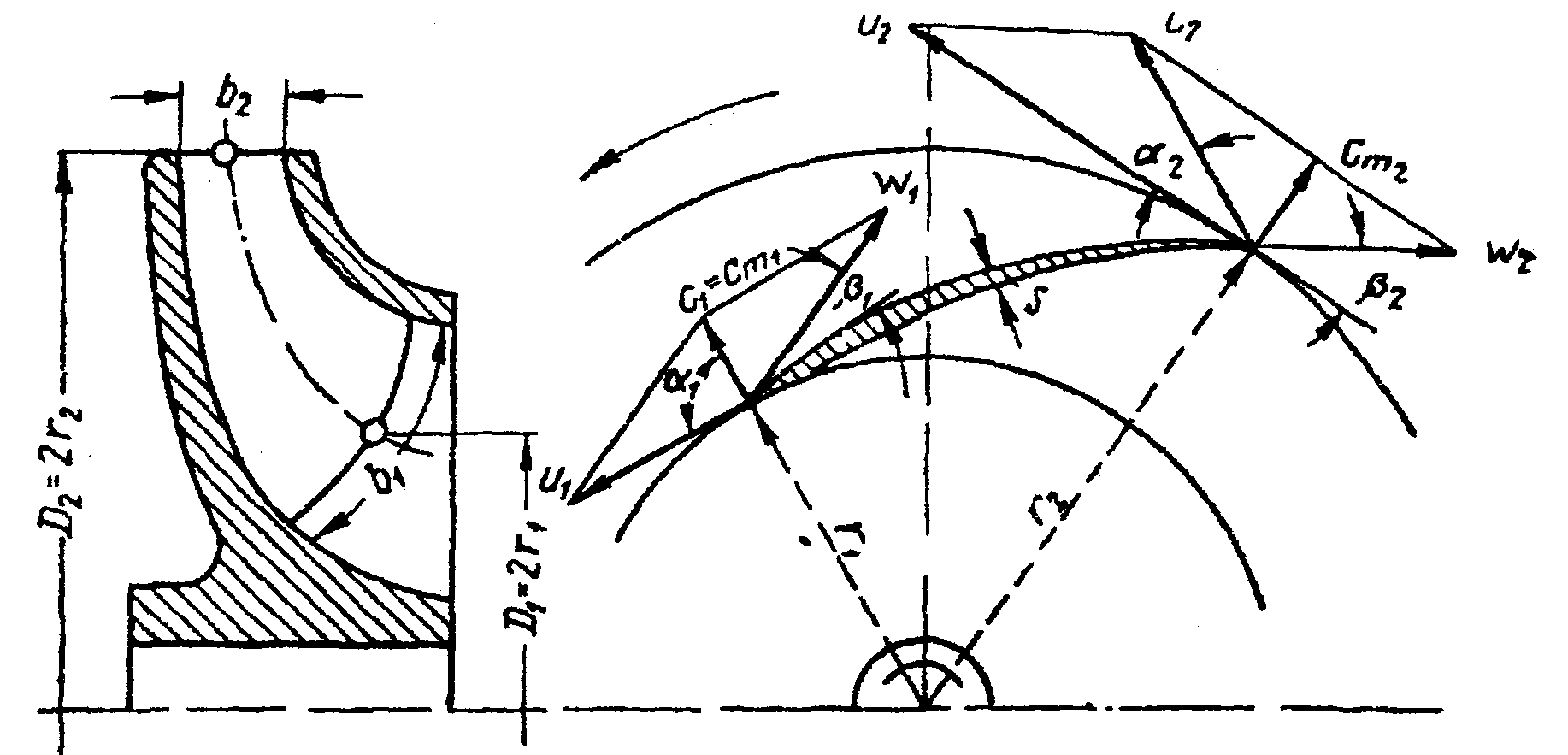
Рис. 2.2. Движение жидкости в каналах рабочего колеса

Угол, образуемый между направлениями абсолютной скоро­сти с и окружной скорости и, обозначают через а. Угол между ка­сательными к лопатке и к окружности в направлении, противопо­ложном направлению окружной скорости, обозначают через 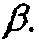Этот угол определяет направление относительной скорости w.

Абсолютную скорость можно рассматривать как результи­рующую двух скоростей:

- с_u совпадающей по направлению с окружной скоростью и являющейся проекцией скорости с на окружную и равной:

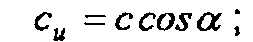
- с_m - меридианальной, направленной по радиусу г и равной:

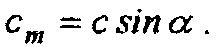
Для скоростей входа и выхода из колеса обозначения одина­ковы, только входным скоростям придается индекс 1, а выходным - индекс 2:

- при входе на лопатки w₁ - относительная скорость, с₁ - аб­солютная скорость, и₁ - окружная скорость;

- при выходе с лопаток w₂ - относительная скорость, с₂ - аб­солютная скорость, и₂ - окружная скорость.

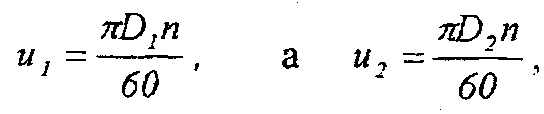
где D₁ - внутренний диаметр рабочего колеса;

D₂ - наружный диаметр рабочего колеса;

п - число оборотов рабочего колеса в минуту.

Следует заметить, что относительные скорости w₁ и w₂ - это те скорости, которые заметил бы наблюдатель, вращающийся с колесом, а абсолютные скорости с₁ и с₂ - это скорости, которые заметил бы наблюдатель, находящийся вне колеса.

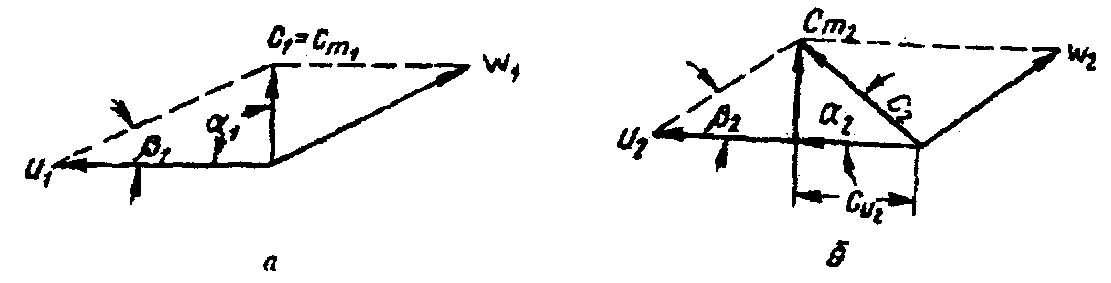
Рис. 2.3. Треугольники скоростей: а - при входе; б - при выходе

Из треугольников скоростей на входе и выходе рабочего ко­леса получим следующие зависимости:

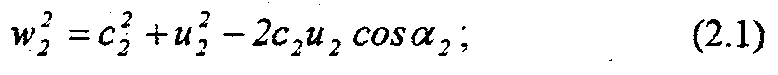
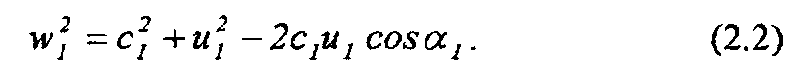
Каждый килограмм жидкости, протекающей через колесо, обладает кинетической энергией (скоростным напором) 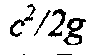и, находясь под давлением р, имеет потенциальную энергию р/у. Если обозначить через р₂ ир₂ соответственно давление при входе и вы­ходе из рабочего колеса, получим полный напор, развиваемый ко­лесом:

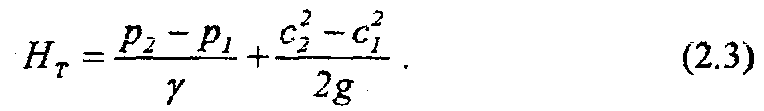
С учетом того, что каждый килограмм жидкости, проходя через рабочее колесо, получает приращение энергии за счет цен­тробежной силы, равной произведению массы частицы на ускоре­ние, то баланс энергии для 1 кг жидкости будет иметь вид:

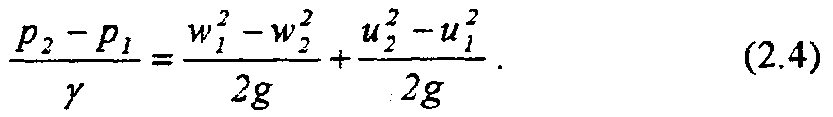
Из уравнений (2.3) и (2.4) получим:

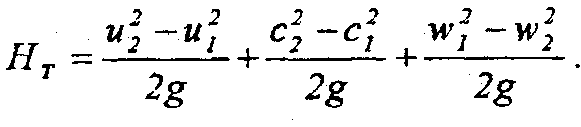
Первый член этого уравнения представляет приращение на­пора, вызываемого центробежными силами, действующими на массы жидкости, перемещающейся от r₁ до r₂ второй член показы­вает изменение кинетической (скоростной) энергии потока от вхо­да до выхода из рабочего колеса. Последний член - это изменение напора в результате изменения относительной скорости потока при протекании жидкости через рабочее колесо.

Пользуясь уравнениями (2.1) и (2.2), заменим w₁ и w₂ соот­ветственно через с₁ , и₁, с₂, и₂. После сокращений получим:

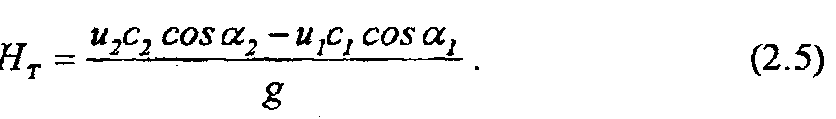
Это и есть основное уравнение Эйлера для определения теоретического напора колеса турбомашины, написанное в самом общем виде и справедливое для всех лопастных машин, т.е. водя­ных, паровых и газовых турбин, центробежных насосов и вентиля­торов, а также турбокомпрессоров. В результате гидравлических сопротивлений протеканию жидкости через рабочее колесо, на преодоление которых затрачивается часть энергии, действитель­ный напор, создаваемый насосом, меньше теоретического. Введя в уравнение (2.5) гидравлический коэффициент полезного действия η_гучитывающий уменьшение теоретического напора, получим значение теоретического напора:

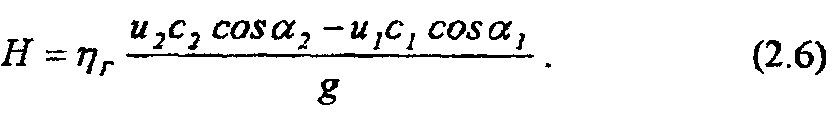
В центробежном насосе во избежание лишних потерь важно соблюдать условие безударного входа жидкости в рабочее колесо. Для этого жидкость подводят к насосу так, чтобы скорость с₀ жид­кости перед входом в колесо была направлена в плоскости, прохо­дящей через ось насоса, и чтобы абсолютная скорость с₁ жидкости не изменялась или же, по возможности, мало отличалась по на­правлению и величине от скорости с₀, т.е. с₁= с₀.

В соответствии с этим а₁ = 90°, второй член правой части равенства (2.6) превратится в нуль, и уравнение Эйлера примет следующий вид:

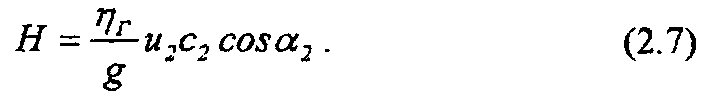
Это и есть основное уравнение центробежного насоса