Лабораторна робота №111. Вивчення обертального руху на маятнику Обербека.

Завдання:експериментально перевірити основний закон динаміки обертального руху твердого тіла (рівняння моментів), що має закріплену вісь обертання.

Приладдя: маятник Обербека; лічильник часу; технічна вага з набором важків; масштабна лінійка; штангенциркуль; набір тягарців різної маси.

Теоретичний матеріал: тангенціальне та кутове прискорення, їх взаємозв’язок ; момент сили; момент інерції матеріальної точки та твердого тіла; момент імпульсу; другий закон Ньютона для поступального та обертального рухів; теорема Гюйгенса – Штейнера.

Література:

1. Р.4. §§. 4.1 - 4.3;

2. Р.1. §§. 1.3 – 1.6; Р.4 §§. 4.1 – 4.6;

3. §§. 2.5, 6.1 – 6.9, 9.1 – 9.7;

4. Р.1 §§. 4 - 5; Р.5 §§. 32 – 37;

5. §§. 8, 9, 19, 21, 31, 32.

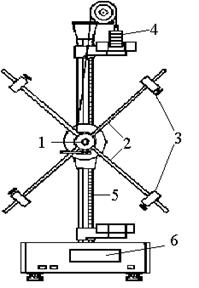
Опис установки.Основною частиною установки (див. рисунок) є маятник Обербека. Він складається з вала, на якому запресовані два шківи 1 різних радіусів 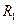і 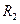та чотири стержні у вигляді хрестовини 2. На стержнях можна закріплювати додаткові тягарці 3 однакової маси 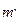. Маятнику надає обертального руху тягарець 4, підвішений до нитки, другий кінець якої намотується на один зі шківів. Висоту опускання тягарця визначають за шкалою, а час опускання – за лічильником часу (механічним, електромеханічним чи електронним секундоміром), який вмикається і вимикається автоматично або вручну.

Виведення робочих формул.Основний закон динаміки обертального руху (другий закон Ньютона для обертального руху, або рівняння моментів) 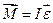перевіряють у два етапи.

Під час першого етапу перевіряють справедливість рівності 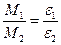, якщо 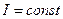. Нехтуючи силами тертя, запишемо рівняння обертального руху маятника

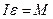, (1)

де I – момент інерції маятника відносно нерухомої осі обертання; 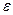- проекція кутового прискорення на вісь обертання (дорівнює модулю вектора кутового прискорення) ; M – проекція моменту сили на вісь обертання (модуль моменту сили).

Момент сили

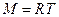, (2)

де R – радіус шківа, на який намотана нитка; T – числове значення сили натягу нитки під час дії на неї тягарця масою m.

Рівняння поступального руху тягарця m має вигляд

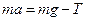, (3)

де a – прискорення тягарця; g – прискорення вільного падіння.

З рівнянь (1) і (2)

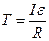(4)

Врахувавши, що 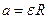, перепишемо останнє рівняння

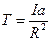(5)

Підставимо вираз (5) у формулу (3), тоді

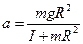(6)

Вважаючи рух тягарця рівноприскореним, прискорення визначаємо за формулою

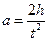(7)

де h – висота, на яку опустився тягарець за час t.

Прирівнявши (6) і (7), отримуємо

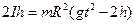. (8)

Зберігаючи сталим момент інерції I маятника та висоту h, поміняємо момент сили М, змінюючи масу тягарців і радіуси шківів, на які намотується нитка. Тоді на основі рівняння (8) можемо записати систему рівнянь

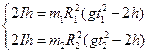(9)

Для зручності записів введемо позначення

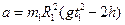
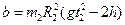(10)

Записані вирази є першими робочими формулами в цій роботі.

Переконавшись, що 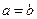, ми переконуємось у прямо пропорційній залежності між результуючим моментом сили і кутовим прискоренням

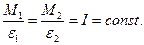
Під час другого етапу перевірки основного закону обертального руху залишимо сталими масу тягарця 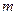і радіус шківа 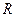, а будемо змінювати момент інерції маятника, змінюючи положення додаткових тягарців масою 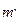на стержнях.

Якщо 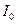- момент інерції маятника (без тягарців 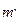) відносно осі обертання, 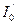- сума моментів інерції чотирьох тягарців масою 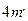відносно осей, які проходять через їхні центри мас, то з віддаленням цих тягарців (їхніх центрів мас) уздовж стержнів на відстань 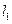від попередньої осі згідно з теоремою Гюйгенса – Штейнера сумарний момент інерції маятника

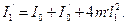(11)

Під час віддалення центрів мас чотирьох тягарців 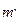на відстань 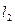від осі обертання

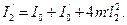(12)

якщо 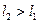, то

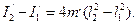(13)

Враховуючи рівняння (1), можемо записати

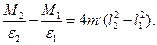(14)

Виразимо ліву частину рівняння (14) через величини, які безпосередньо вимірюємо під час експерименту. Для цього використаємо рівняння (7), яке при двох змінних значеннях 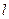буде мати такий вигляд:

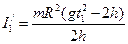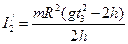; , (15)

звідки

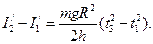(16)

З формул (13) і (16) оотримуємо

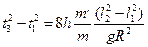(17)

де 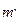- маса одного тягарця на стержнях; m – маса тягарця, підвішеного до нитки, намотаної на шків радіусом 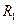або 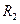; 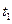, 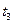– час опускання тягарців з висоти 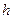, якщо тягарці розміщені, відповідно, на відстані 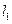, від осі обертання.

Уведемо такі позначення :

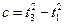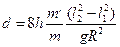; . (18)

Вирази для с і d є відповідно третьою та четвертою робочими формулами в цій лабораторній роботі, а підтвердження рівності (17) є підтвердженням обернено пропорційної залежності між моментом інерції і кутовим прискоренням, тобто правильності основного закону обертального руху.