ОДНОРАЗРЯДНЫЙ ПОЛУСУММАТОР.
Условное обозначение:
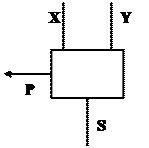
В двоичной системе счисления операция сложения двух двоичных чисел в одном разряде осуществляется по правилу:
| X | Y | P(перенос) | S(сумма) |
Из таблицы видно, что P(X,Y) = X&Y. Формула для S можно получить двумя способами: либо по алгоритмам получения СДНФ или СКНФ, либо по сводной таблице логических функций двух переменных
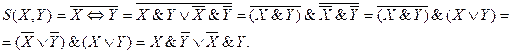
Предпоследняя формула – это СКНФ, последняя – СДНФ.
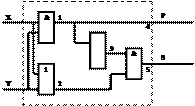
Для построения функциональной схемы воспользуемся структурной формулой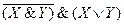 
, так как в ней наименьшее количество операций. Получим структурные формулы и функциональную схему одноразрядного полусумматора: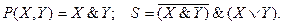 
СВОДНАЯ ТАБЛИЦА ЛОГИЧЕСКИХ ФУНКЦИЙ ДВУХ ПЕРЕМЕННЫХ
| ЗНАЧЕНИЯ ФУНКЦИИ F(X,Y) | НАЗВАНИЕ ФУНКЦИИ | ОБОЗНАЧЕНИЕ ФУНКЦИИ | |||
| X=0 Y=0 | X=0 Y=1 | X=1 Y=0 | X=1 Y=0 | ||
| Константа 0 |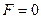 
| ||||
| Конъюнкция |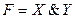 
| ||||
| Отрицание импликации XY | 
| ||||
| Переменная X |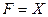 
| ||||
| Отрицание импликации YX | 
| ||||
| Переменная Y |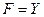 
| ||||
| Отрицание эквивалентности | 
| ||||
| Дизъюнкция |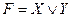 
| ||||
| Отрицание дизъюнкции |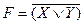 
| ||||
| Эквивалентность |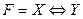 
| ||||
| Отрицание Y |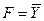 
| ||||
| Импликация YX |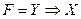 
| ||||
| Отрицание X |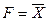 
| ||||
| Импликация XY |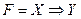 
| ||||
| Отрицание конъюнкции |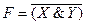 
| ||||
| Константа 1 |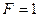 
|
Проверить правильность построения схемы можно описав работу, полученного логического устройства с помощью таблицы истинности:
| Входы | Выходы | |||||
| X | Y | |||||
Из таблицы видно, что значения на выходах 4 и 5 соответствуют значениям переноса и суммы при сложении двоичных чисел.
Дата добавления: 2015-09-11; просмотров: 1817;