Одноразрядный полусумматор

Сумматоры

Сумматоры выполняют арифметическую операцию сло­жения двух чисел.

Они имеют как самостоятельное значение, так и явля­ются составной частью арифметическо-логического устрой­ства (АЛУ). При организации различных вычислительных процессов суммированию отводится главная роль, оно яв­ляется основной операцией. Например, вычитание — это суммирование с использованием дополнительного либо обратного кода, умножение сводится к сдвигу и сложе­нию (суммированию) двоичных чисел. Следует отметить, что сумматоры являются логическими устройствами, фун­кционируют по законам алгебры логики, но выполняют операцию арифметического, а не логического сложения.

В соответствии с определением, сумматор суммирует два числа. Выходной сигнал зависит только от двух вход­ных сигналов, действующих на входе в текущий момент. Следовательно, сумматор является комбинационным уст­ройством. Однако, некоторые сумматоры, например, на­капливающий сумматор и другие, содержат в своем соста­ве элементы памяти.

По числу выводов различают: полусумматоры, одно­разрядные сумматоры, многоразрядные сумматоры.

Полусумматор имеет два входа и два выхода, предназ­начен для сложения двух одноразрядных слов и формиру­ет на своих выходах сигнал суммы и сигнал переноса в старший разряд.

Одноразрядный сумматор имеет три входа и два выхо­да, предназначен для сложения двух одноразрядных слов и формирует сигнал выхода и сигнал переноса в старший разряд из входных слов и сигнала переноса из младшего разряда.

Многоразрядный сумматор предназначен для сложе­ния многоразрядных слов.

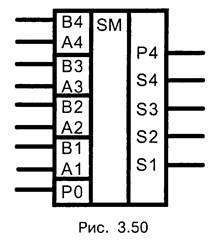
В настоящее время выпускают микросхемы одно-, двух- и четырехразрядные сумматоры. Маркировку микросхем — сумматоров можно определить по буквам ИМ — функци­ональное назначение, например, К555ИМ6 — четырехраз­рядный полный двоичный сумматор. На принципиальных схемах сумматоры обозначают буквами SM (рис. 3.50).

В зависимости от способа обработки чисел сумматоры разделяются на сумматоры последовательного и параллель­ного типов. Сложение чисел в последовательных суммато­рах осуществляется поразрядно, последовательно во времени.

В сумматорах параллельного действия сложение всех разрядов многоразрядных чисел происходит одновременно.

По способу тактирования различают синхронные и асинхронные сумматоры. В синхронных сумматорах опе­рация сложения осуществляется по тактовым импульсам, и время ее проведения не зависит от длины разрядов ко­дов, остается постоянным. В асинхронных сумматорах время выполнения операции зависит от длины входных кодов и поэтому необходимо формировать признак окон­чания операции.

В зависимости от используемой системы счисления различают двоичные, двоично-десятичные и другие типы сумматоров.

В виду особой важности сумматоров разработано боль­шое количество разнообразных схем на основе различных алгоритмов синтеза. Рассмотрим наиболее характерные схемы построения сумматоров.

Одноразрядный полусумматор

В сумматорах операция суммирования чисел, представ­ленных в двоичном коде, осуществляется поразрядно.

Простейший случай — это суммирование двух однораз­рядных слов. В десятичной системе

0 + 0 = 0; 0 + 1 = 1; 1 + 0 = 1; 1 + 1 = 2; (3.35) что соответствует в двоичной системе счисления

0 + 0 = 0; 0 + 1 = 1; 1+ 0 = 1; 1 + 1 = 10. (3.36)

В последнем случае результат суммы оказался двух­разрядным 10₂= 2₁₀. Обычное явление, когда при сумми­ровании двух чисел в любой системе счисления результат имеет на один разряд больше. В двоичной системе едини­ца в старшем разряде суммы называется единицей пере­носа. Сведем формулы (3.36) в таблицу.

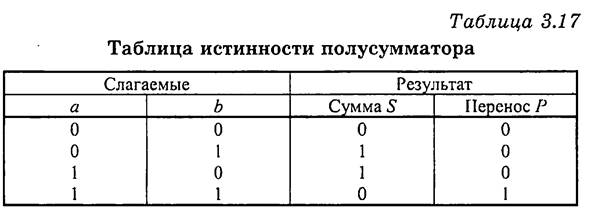
Из таблицы 3.17 получим аналитические выражения для суммы S и переноса Р

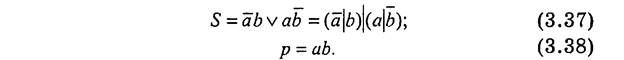
Выражение для S можно записать с помощью извест­ной операции ИСКЛЮЧАЮЩЕЕ-ИЛИ

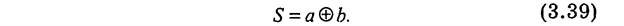
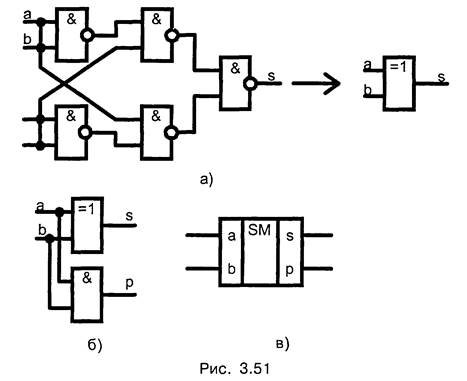
Техническая реализация полусумматора на основе (3.37) — (3.39) представлена на рис. 3.51.

Используя представление в базисе ИЛИ-НЕ, из табли­цы 3.17 получим

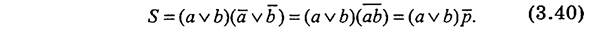
На основе формулы (3.40) построим схему полусумма­тора, содержащего меньшее число логических элементов (рис. 3.52)

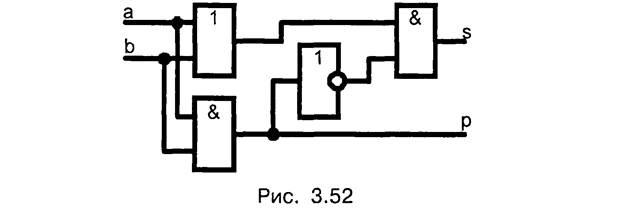
В то же время схема (рис. 3.52) содержит различные элементы: И, НЕ, ИЛИ.

Полусумматор (рис. 3.51; 3.52) не имеет входа перено­са с предыдущего разряда, поэтому его можно использо­вать только в младших разрядах устройства обработки мно­горазрядных двоичных слов.

Составим таблицу истинности сложения одного разря­да многоразрядного двоичного слова с учетом переноса из младшего разряда (таблица 3.18).

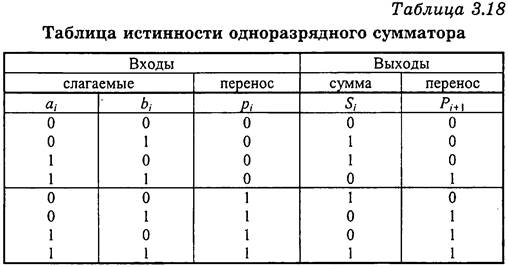
Пользуясь таблицей истинности 3.18 в базисе И-ИЛИ­-НЕ получаем выражения для

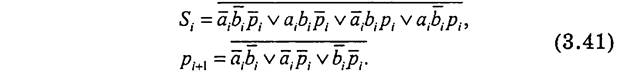
С другой стороны, составляем совершенную дизъюнк­тивную нормальную форму

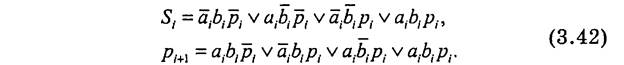
После преобразований (3.42), используя функции «рав­нозначность» (ИСКЛЮЧАЮЩЕЕ ИЛИ-HE), «неравноз­начность» (ИСКЛЮЧАЮЩЕЕ ИЛИ), получим

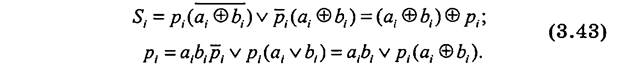
Полный одноразрядный сумматор в соответствии с (3.43) построим из двух полусумматоров (рис. 3.53)

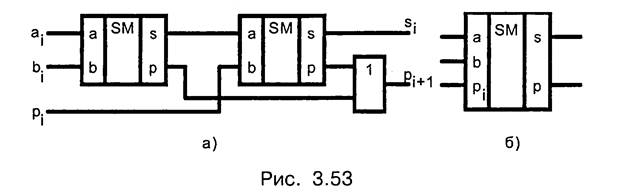
Полные одноразрядные сумматоры являются основой, из которых получают различные схемы многоразрядных сумматоров.