СОВЕРШЕННАЯ ДИЗЪЮНКТИВНАЯ НОРМАЛЬНАЯ ФОРМА И СОВЕРШЕННАЯ КОНЪЮНКТИВНАЯ НОРМАЛЬНАЯ ФОРМА.
Известно два способа задания логических функций: с помощью формулы и с помощью таблицы истинности. По формуле легко составляется таблица. На практике при конструировании различных электронных устройств часто возникает обратная задача – от таблицы истинности перейти к формуле, чтобы на ее основе построить функциональную схему.
Введем следующие определения:
Элементарной конъюнкцией называется конъюнкция нескольких переменных, взятых с отрицанием или без отрицания, причем среди переменных могут быть одинаковые.
Элементарной дизъюнкцией называется дизъюнкция нескольких переменных, взятых с отрицанием или без отрицания, причем среди переменных могут быть одинаковые.
Всякую дизъюнкцию элементарных конъюнкций назовем дизъюнктивной нормальной формой (ДНФ).
Всякую конъюнкцию элементарных дизъюнкций назовем конъюнктивной нормальной формой (КНФ).
Совершенной дизъюнктивной нормальной формой (СДНФ) называется ДНФ, в которой нет одинаковых элементарных конъюнкций и все конъюнкции состоят из одного и того же набора переменных, в который каждая переменная входит только один раз (возможно, с отрицанием).
Совершенной конъюнктивной нормальной формой (СКНФ) называется КНФ, в которой нет одинаковых элементарных дизъюнкций и все дизъюнкции состоят из одного и того же набора переменных, в который каждая переменная входит только один раз (возможно, с отрицанием).
Приведем примеры формул, соответствующих и не соответствующих этим определениям:
| НАЗВАНИЕ ФОРМУЛЫ В ОПРЕДЕЛЕНИИ | Формула, соответствующая определению | ФОРМУЛА, НЕ СООТВЕТСТВУЮЩАЯ ОПРЕДЕЛЕНИЮ |
| Элементарная дизъюнкция | 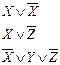
| 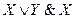
|
| Элементарная конъюнкция | 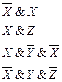
| 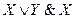
|
| ДНФ | 
| ДНФ можно построить для всякой формулы (путем преобразования) |
| КНФ | 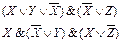
| КНФ можно построить для всякой формулы (путем преобразования) |
| СДНФ | 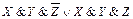
| 
|
| СКНФ | 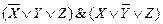
| 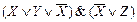
|
Дата добавления: 2015-09-11; просмотров: 1383;
