Любую функцию, кроме констант 0 и 1, можно представить в виде как СДНФ, так и СКНФ.
Этот факт является теоремой алгебры логики. Из него следует, что любая формула (кроме констант 0 и 1) может быть преобразован к виду как СДНФ, так и СКНФ. Константа 0 может быть представлена только СКНФ (  ), а константа 1 – только СДНФ (
), а константа 1 – только СДНФ ( 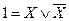 ). Из вышесказанного следует, что если надо построить формулу некоторой функции по таблице истинности этой функции, то всегда можно получить СКНФ или СДНФ этой функции.
). Из вышесказанного следует, что если надо построить формулу некоторой функции по таблице истинности этой функции, то всегда можно получить СКНФ или СДНФ этой функции.
Алгоритм получения СДНФ по таблице истинности:
- Отметить те строчки таблицы истинности, в последнем столбце которых стоят 1:
| X | Y | F(X,Y) |
| 0 | 0 | |
| 0 | 1 | 1* |
| 1 | 0 | 1* |
| 1 | 1 | 0 |
- Выписать для каждой отмеченной строки конъюнкцию всех переменных следующим образом: если значение некоторой переменной в данной строке равно 1, то в конъюнкцию включать саму эту переменную, если равно 0, то ее отрицание:
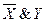 – для 2-й строки;
– для 2-й строки;
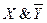 – для 3-й строки.
– для 3-й строки.
- Все полученные конъюнкции связать в дизъюнкцию:
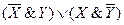 .
.
Алгоритм получения СКНФ по таблице истинности:
- Отметить те строки таблицы истинности, в последнем столбце которых стоит 0:
| X | Y | F(X,Y) |
| 0 | 0* | |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0* |
- Выписать для каждой отмеченной строки дизъюнкцию всех переменных следующим образом: если значение некоторой переменной в данной строке равно 0, то в дизъюнкцию включать саму эту переменную, если равно 1, то ее отрицание:
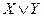 – для 1-й строки;
– для 1-й строки;
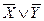 – для 4-й строки.
– для 4-й строки.
- Все полученные дизъюнкции связать в конъюнкцию:
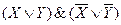 .
.
Покажем, что полученные по двум алгоритмам СДНФ и СКНФ эквивалентны. Преобразуем СКНФ по правилам алгебры логики:  .
.
Примечание: для нахождения формулы по таблице истинности рекомендуется использовать тот из двух алгоритмов, в котором в таблице помечается меньше строк.
Дата добавления: 2015-09-11; просмотров: 1035;
