Кинематические уравнения в обобщенных координатах. Углы Эйлера, Крылова, кватернионы.
В курсе теоретической механики сферическое движение задавалось углами Эйлера (рис. 1.2) – углом прецессии y (поворот вокруг неподвижной оси Oz), углом нутации q (поворот вокруг полуподвижной оси ОК – линии пересечения плоскостей Oxy и Oξη, называемой линией узлов) и углом собственного вращения j (поворот вокруг связанной с телом оси Oz).
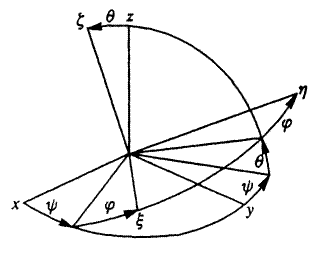
Рис. 1.2. Система ориентационных углов Эйлера твердого тела
Углы Эйлера перечислены здесь в порядке поворотов, которые надо совершить над неподвижной СК Oxyz чтобы она совместилась с подвижной СК Oξηζ. Использование углов Эйлера в сферическом движении делалось для демонстрации принципиальной возможности решения соответствующих задач кинематики. Здесь же у нас стоит задача более оптимально описать такое движение. Кинематические соотношения, выражающие проекции угловой скорости тела на оси связанной СК через угловые скорости указанных углов представляются для углов Эйлера формулами (сверены с программой КИДИМ):
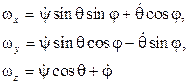 (1.1)
(1.1)
Несмотря на лаконичность такого задания положения тела при сферическом движении (3 степени свободы, 3 координаты), в современной механике оно используется редко. Это объясняется, в частности тем, что формулы вычисления обобщенных скоростей через проекции угловой скорости тела (обратные кинематические соотношения) содержат особенности и несимметричны, что затрудняет анализ результатов и приводит к вычислительным погрешностям. Для углов Эйлера эти соотношения представляются формулами:
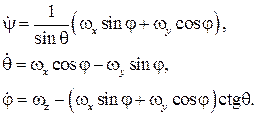 (1.2)
(1.2)
Более предпочтительным является использование параметров Родрига-Гамильтона, кватернионов, параметров Кейли-Клейна.
Докажем теорему д’Аламбера-Эйлера.
Перемещение тела, имеющего неподвижную точку, из одного положения в другое, можно осуществить поворотом вокруг некоторой оси, проходящей через неподвижную точку.
Движение тела полностью определяется движением любого треугольника, принадлежащего телу. Поэтому для сферического движения это эквивалентно движению двух точек на некоторой сфере, центр которой совпадает с неподвижной точкой, или движению дуги, соединяющей эти точки. Предположим, что в результате перемещения тела за время Dt некоторая точка А переместилась по сфере в положение В (рис. 1.3). В то же самое время точка, которая находилась в положении В, заняла новое положение С.
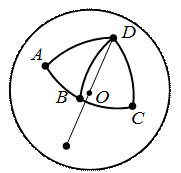 Рис. 1.3.
Рис. 1.3.
| Плоскость ABC пересекает неподвижную сферу по окружности (малого или большого круга). Если D один из полюсов этого круга на сфере, то 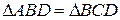 , т.к. они равнобедренные сферические и , т.к. они равнобедренные сферические и 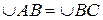 , так как они являются двумя положениями одной и той же дуги сферы АВ. , так как они являются двумя положениями одной и той же дуги сферы АВ. 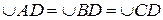 по построению (равноудалены от полюса). Следовательно, по построению (равноудалены от полюса). Следовательно, 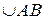 может быть совмещена с может быть совмещена с 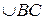 при помощи вращения вокруг оси OD на угол ADB. Теорема доказана. при помощи вращения вокруг оси OD на угол ADB. Теорема доказана.
|
Параметры Родрига-Гамильтона. Для задания такого поворота, который будем называть конечным поворотом тела, очевидно, надо задать положение оси, направление и угол поворота. Ось поворота можно задать единичным вектором, направленным в ту сторону, откуда поворот тела будет наблюдаться против часовой стрелки. Этот вектор определится своими проекциями на оси некоторой СК (направляющими косинусами его углов с осями этой СК). Таким образом, конечный поворот определится четырьмя скалярными величинами ‑ проекциями единичного вектора оси и величиной угла самого поворота вокруг этой оси.
Воспользуемся для задания таких четырех величин параметрами Родрига-Гамильтона, которые обозначим здесь λ0, λ1, λ2, λ3. Последние три параметра обычно объединяют в вектор 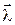 ={λ1, λ2, λ3}T. Таким образом, будем рассматривать совокупность скалярной и векторной величин λ0,
={λ1, λ2, λ3}T. Таким образом, будем рассматривать совокупность скалярной и векторной величин λ0, 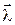 . Эти параметры вводятся через элементы конечного поворота и могут быть определены следующим образом. Пусть
. Эти параметры вводятся через элементы конечного поворота и могут быть определены следующим образом. Пусть 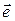 ‑ направляющий орт оси, вокруг которой поворот совершается, а ψ ‑ величина угла поворота. Тогда
‑ направляющий орт оси, вокруг которой поворот совершается, а ψ ‑ величина угла поворота. Тогда
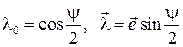 .
.
Очевидно, что 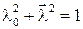 . Отметим, что, как следует из способа введения параметров Родрига-Гамильтона, параметры
. Отметим, что, как следует из способа введения параметров Родрига-Гамильтона, параметры 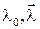 и
и 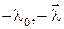 характеризуют один и тот же конечный поворот и в этом смысле геометрически тождественны.
характеризуют один и тот же конечный поворот и в этом смысле геометрически тождественны.
Не останавливаясь на анализе свойств и применении введенных таким образом параметров Родрига-Гамильтона, рассмотрим еще более обобщающие величины для этого – кватернионы.
Дата добавления: 2015-09-11; просмотров: 5850;
