Вращение точки вокруг фронтально-проецирующей оси
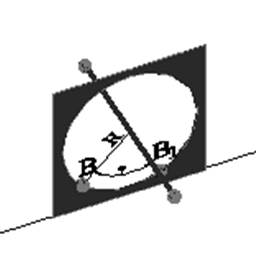
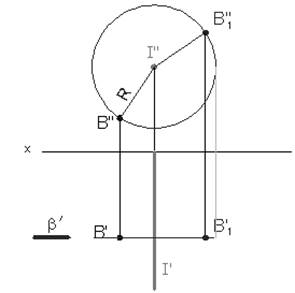
Рисунок 6
При вращении вокруг фронтально-проецирующей оси точка движется по окружности, плоскость которой перпендикулярна оси вращения i (рисунок 6). Ось i перпендикулярна плоскости p 2 , следовательно, фронтальная проекция точки перемещается по окружности, а горизонтальная – по прямой, перпендикулярной горизонтальной проекции оси вращения. Это след плоскости окружности, по которой перемещается точка.
i (i’, i’’) ┴ p2;
R – радиус вращения;
β – фронтальная плоскость, в которой перемещается точка;
B (B’, B”) – исходное положение точки;
B1 (B1’,B1”) – новое положение точки после поворота.
Пример: Определить действительную величину отрезка способом вращения.
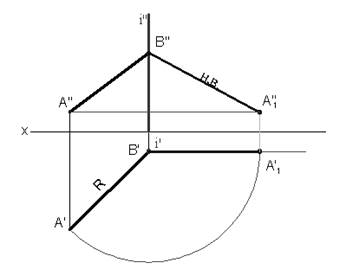
Рисунок 7
Для решения задачи (рисунок 7)необходимо повернуть отрезок до положения параллельного плоскости p1 или p2. Для этого задается ось вращения, перпендикулярная p2 или p1. Для упрощения решения рекомендуется ось вращения проводить через один из концов отрезка. В этом случае этот конец отрезка остается неподвижным, а вращается только второй конец отрезка.
В данном случае выбрана осьi перпендикулярная плоскости p1 и проходящая через точку B – один из концов отрезка. Точка A перемещается по окружности, которая на плоскость p1 проецируется в окружность, а на плоскость p2 – в прямую линию, перпендикулярную фронтальной проекции оси вращения i.
B’A1’ || Оx – новое положение горизонтальной проекции отрезка после поворота;
B”A1” – новое положение фронтальной проекции, которая является действительной величиной отрезка.
Пример: Определить действительную величину четырёхугольника ABCD способом вращения (рисунок 8).
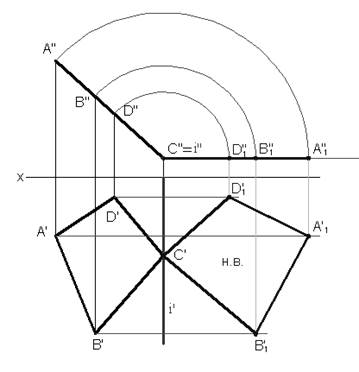
Рисунок 8
Так как четырёхугольник ABCD перпендикулярен плоскости p2, выбирается ось вращения также перпендикулярная p2. Для упрощения решения ось вращения i проводим через одну из вершин четырёхугольника, например, через точку C. Новая фронтальная проекция ABCD после поворота займет положение параллельное оси Оx. Горизонтальные проекции вершин четырёхугольника строятся с помощью вертикальных и горизонтальных линий связи.
- Способ плоскопараллельного перемещения
Плоскопараллельным перемещением геометрического объекта называется такое перемещение, когда точки этого объекта перемещаются в плоскостях, каждая из которых параллельна какой-либо плоскости проекций.
При этом проекция этого объекта на плоскость параллелизма изменяет свое положение без изменения формы и размеров.
Пример: Определить действительную величину отрезка и преобразование его в проецирующий способом плоскопараллельного перемещения (рисунок 9).

Рисунок 9
В этом случае отрезок прямой АВ перемещаем так, что все его точки остаются в плоскостях, параллельных плоскости П1. При этом А'1В'1=А1В1, а фронтальные проекции траекторий точек А и В-прямые, параллельные оси X, вторым плоскопараллельным перемещением ставим отрезок в горизонтально-проецирующее положение, при этом А'2В'2=А''2В''2 , а горизонтальные проекции точек А и В-прямые, параллельные оси X.
Пример: Преобразовать плоскость общего положения в плоскость уровня способом плоскопараллельного перемещения (рисунок 10).
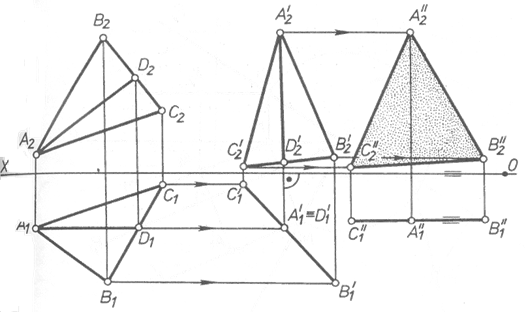
Рисунок 10
Выполнено последовательно два плоскопараллельных перемещения треугольника АВС: сначала относительно оси, перпендикулярной к плоскости проекций П2 , потом относительно оси, перпендикулярной к плоскости П1. При первом плоскопараллельном перемещении плоскость треугольника преобразована в горизонтально-проецирующую, при этом фронталь AD треугольника переведена в горизонтально-проецирующее положение (A'2D'2 ^X).
Другим плоскопараллельным перемещением треугольник А'В'С' преобразован в треугольник А''В''С'', при этом фронтальная проекция А''2 В''2 С''2 определяет действительный размер треугольника АВС.
- Способ прямоугольного треугольника
Действительная величина отрезка есть гипотенуза прямоугольного треугольника, у которого один катет есть горизонтальная (или фронтальная) проекция отрезка, а второй катет – разность координат концов отрезка до горизонтальной ▲z (или фронтальной ▲y) плоскости проекций (рисунок 11).

Рисунок 11
Пример: Определить действительную величину отрезка AB способом прямоугольного треугольника (рисунок 12).
Для решения задачи прямоугольный треугольник можно построить на горизонтальной или фронтальной проекции с использованием разности координат ▲z или ▲y, а также на свободном поле чертежа.
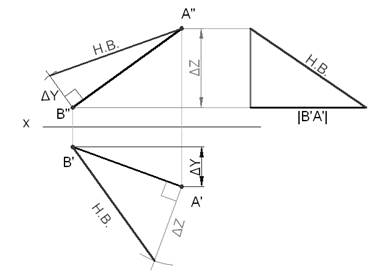
Рисунок 12
Контрольные вопросы:
1. Какие способы преобразования комплексного чертежа вы знаете?
2. В чем сущность способа замены плоскостей проекций?
3. В чем сущность способа плоско-параллельного перемещения?
4. Зачем осуществляют преобразование комплексного чертежа?
5. Чем отличаются способы преобразования комплексного чертежа?
6. Назовите четыре исходные задачи, решаемые способом замены плоскостей проекций?
7. Как преобразовать прямую общего положения в проецирующую?
8. Как способом замены плоскостей проекций определить углы наклона плоскости общего положения к плоскостям проекций?
9. Сколько раз необходимо произвести замену плоскостей проекций для преобразования плоскости общего положения в плоскость уровня?
10. Запишите алгоритм способа замены плоскостей проекций?
Дата добавления: 2015-09-11; просмотров: 2951;
