Способ замены плоскостей проекций. Методы преобразования на чертеже.

Лекция № 6

Методы преобразования на чертеже.

План:

Способ замены плоскостей проекций

Способ вращения.

Способ плоско-параллельного перемещения.

Способ треугольника.

Решение многих задач начертательной геометрии упрощается, если гео­метрические объекты занимают относительно плоскостей проекций некоторое частное положение. Например, если геометрический объект (прямая, плоская фигура) расположен в плоскости, параллельной плоскости проекций, то на эту плоскость он проецируется в натуральную величину, что позволяет очень просто решать метрические задачи, связанные с определением натуральных размеров геометрических объектов. А вот при определении расстояния от точки до плос­кости удобно, чтобы плоскость была проецирующей.

В связи с этим возникает следующая идея решения метрических и позиционных задач начертательной геометрии: посредством изменения взаимного положения геометрических объектов и плоскостей проекций добиться удобного для данного конкретного случая относительного положения.

Этого можно добиться двумя способами:

Положение оригинала в пространстве остается неизменным, а заменяют одну или обе плоскости проекций (способ замены плоскостей проекций);

Неизменной остается система плоскостей проекций, а меняют положение оригинала в пространстве (способы плоскопараллельного перемещения и вращения).

Способ замены плоскостей проекций

Сущность способа заключается в том, что система плоскостей проекций p₁^p₂ дополняется плоскостями p4, p5, которые образуют с плоскостями p₂ или p₁ или между собою новую систему взаимно перпендикулярных плоскостей проекций. При этом геометрические фигуры остаются в пространстве неподвижными.

Замена фронтальной плоскости p₂ на p₄.

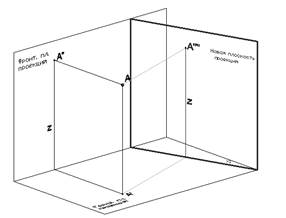
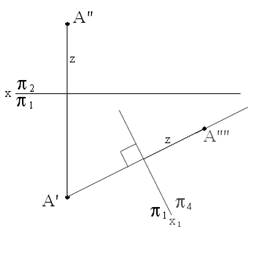
Рисунок 1

Плоскость p₁ и точка A остаются неизменными, поэтому будут неизменными расстояние точки до горизонтальной плоскости проекций (рисунок 1) , то есть координата Z, и горизонтальная проекция точки. Для построения новой проекции точки на плоскости p4 необходимо с неизменной горизонтальной проекции точки провести линию связи, перпендикулярную новой оси Ox, на которой необходимо отложить длину неизменной координаты Z. A’’’’ – новая проекция точки A.