Основные формулы комбинаторики.

ОСНОВНЫЕ ПОНЯТИЯ

Оглавление.

1. Основные формулы комбинаторики.

2. Случайные события. Частота. Вероятность.

3. Аксиомы вероятностей.

4. Классическое определение вероятности.

5. Условная вероятность. Теорема умножения вероятностей.

6. Формула полной вероятности.

7. Формула Бейеса.

Основные формулы комбинаторики.

Комбинаторика изучает количества комбинаций, подчиненных определенным условиям, которые можно со­ставить из элементов, безразлично какой природы, задан­ного конечного множества. При непосредственном вычис­лении вероятностей часто используют формулы комбина­торики. Ниже приведены самые распространенные из них:

Перестановками называют комбинации, состоящие из одних и тех же 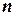различных элементов и отличающиеся только порядком их расположения. Число всех возмож­ных перестановок:

, .

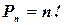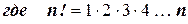По определению, .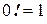

Размещениями называют комбинации, составленные из 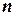различных элементов по 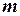элементов, которые от­личаются либо составом элементов, либо их порядком. Число всех возможных размещений

.

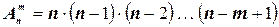Либо .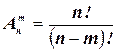

Сочетаниями называют комбинации, составленные из 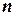различных элементов по 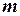элементов, которые отли­чаются хотя бы одним элементом. Число сочетаний

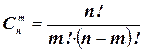
Числа размещений, перестановок и сочетаний связаны равенством

.

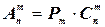Замечание: выше предполагалось, что все 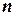элементов раз­личны. Если же некоторые элементы повторяются, то в этом случае комбинации с повторениями вычисляют по другим формулам.

Напри­мер, если среди 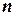элементов есть 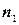элементов одного вида, 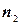эле­ментов другого вида и т. д., то число перестановок с повторениями:

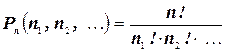, где .

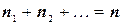При решении задач комбинаторики используют сле­дующие правила:

Правило суммы: если некоторый объект 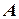может быть выбран из совокупности объектов 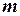способами, а другой объект 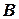может быть выбран 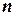способами, то выбрать либо 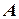, либ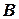о можно 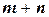способами.

Правило произведения: если объект 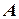можно выбрать из совокупности объектов 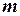способами и после каждого такого выбора объект 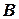можно выбрать 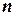спо­собами, то пара объектов 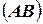в указанном порядке может быть выбрана 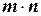способами.

2. Случайные события. Частота. Вероятность.

Теория вероятностей — математическая наука, изучающая закономерности массовых, случайных явлений (событий).

Случайным событием (или просто событием) называется всякое явление, которое может произойти или не произойти при осуществлении определенной совокупности условий. Теория вероятностей имеет дело с такими событиями, которые имеют массовый характер. Это значит, что данная совокупность условий может быть воспроизведена неограниченное число раз. Каждое такое осуществление данной совокупности условий называют испытанием (или опытом).

Если, например, испытание состоит в бросании монеты, то выпадение герба является событием. Если испытание — изготовление подшипника данного типа, то соответствие подшипника стандарту — событие. Если испытание — бросание игральной кости, т. е. кубика, на гранях которого проставлены цифры (очки) от 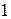до 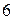, тo выпадение пятерки — событие.

При подбрасывании монеты вероятность выиграть составляет 1/2, а при бросании игральной кости выигрышем считается выпадение цифры шесть (вероятность выигрыша 1/6). Чему равна вероятность проигрыша в каждом случае? Значит ли это, что играть в кости менее выгодно?