Действие сосредоточенной силы. Задача Буссинеска.

Рассмотрим действие сосредоточенной силы Р, приложенной перпендикулярно к ограничивающей полупространство плоскости. Будем считать полупространство однородным в глубину и в стороны и линейно-деформируемым. Задача заключается в определении всех составляющих напряжений для любой точки полупространства. Эта задача впервые была решена проф. Ж. Буссинеском (1885 г.)

Возьмем точку М, определяемую полярными координатами R и β.

Рис.13. Схема к определению напряжений при действии сосредоточенной силы (основная задача).

Для упрощения вывода принимают как постулат, что напряжение σ_R пропорционально cos β и обратно пропорционально квадрату расстояния от точки приложения до сосредоточенной силы R². Т.о.

;

где А –коэффициент, определяемый из условий равновесия:

.

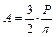Подставляя это значение в формулу выше, получим:

-

это общая формула векторного напряжения в любой точке пространства от действия сосредоточенной нагрузки в однородных грунтах.

Отнесем величину радиальных напряжений не к площадке перпендикулярной радиусу, а к площадке, параллельной ограничивающей плоскости и составляющей с ней угол β:

;

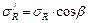или подставляя значение σ_R и принимая во внимание, что cos β = z/R получим:

.

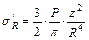Далее, не меняя направление площадки, разложим силу на три направления: одно z – перпендикулярное площадке и два х и у – лежащих в плоскости площадки.

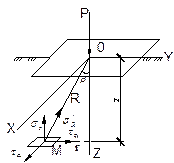
Рис.14. Определение составляющих напряжений по горизонтальной