Графическая схема моделирования динамики представлена на рисунке 17.
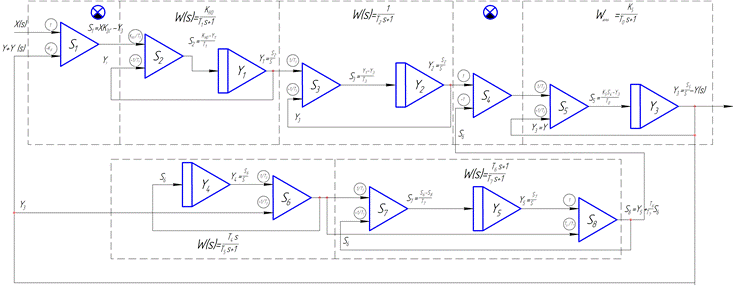
рисунок 17. Графическая схема моделирования динамики
Из рис. 17 видно, что графические модели простейших звеньев, рассматриваемых выше, соединены между собой в соответствии со структурной схемой (рис. 16). Коэффициент передачи тахогенератора Ктг, представляющего собой звено обратной звязи, учтен как коэффициент при входе Y3 сумматора S1. Коэффициенты передачи неохваченного обратной связью участка прямой цепи Кно и охваченного Кy учтены на соответствующих входах сумматора S2 и S5. Охват разомкнутой цепи АЭП осуществляется подачей величины выходной величины Y3=Y, снимаемой с интегратора Y3 на вход сумматора S1. Встраевание корректирующей обратной связи осуществляется аналогично.
При этом на ее вход подается величина Y3, снимаемая с выходного интегратора Y3, а ввод сигнала коррекции в прямую цепь осуществляется с помощью сумматора S4.
Четвертый этап состоит в составлении программы расчета динамики. Последовательная запись рекуррентных выражений для основного цикла программы в нашем конкретном примере по графической схеме рис. 17 имеет вид:
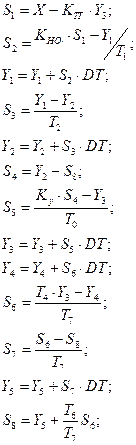
Обратим внимание на зависимости в строках 3, 5, 8, 9, 12. Каждая из них отображает одношаговую процедуру решения дифференциального уравнения методом Эйлера. Шаг интегрирования в данном случае обозначен DT. Данный метод является простейшим и наименее точным, однако он позволяет решать широкий круг задач при проектировании. При необходимости увеличить точность вычислений, проектировщик может применять более точные методы. В данном случае для нас этот вопрос не является принципиальным, т.к точность решения методом Эйлера может быть, при необходимости, значительно повышена за счет уменьшения шага вычислений, что с учетом быстродействия современных ЭВМ не требует больших затрат машинного времени.
Рассмотрим методы численного решения обыкновенных дифференциальных уравнений (ДУ) [11].
Дифференциальным называют уравнения, содержащие одну или несколько производных. К сожалению, лишь немногие их них удается решить без помощи ЭВМ. Поэтому численные методы решения ДУ играют важную роль в практике инженерных расчетов.
Чтобы решить обыкновенное ДУ необходимо знать значение зависимой переменной и (или) ее производных при некоторых значениях независимой переменной. Если эти дополнительные условия задаются при одном значении независимой переменной, то такая задача называется, задай с начальными условиями или задачей Коши. Если же условия задаются при двух и более значениях независимой переменной, то задача называется краево̀й.
Задачу Коши можно сформулировать следующим образом: пусть дано ДУ
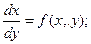
начальное условие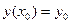 
. Требуется найти функцию y(x), удовлетворяющую как указанному уравнению, так и начальному условию.
Обычно численное решения этой задачи получают, вычисляя сначала значение производной, а затем задавая малое приращение Х и переходя к точке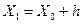 
. Положение новой точки определяется по наклону кривой, вычисленному с помощью ДУ. Таким образом, график численного решения представляет собой последовательность коротких прямолинейных отрезков, которыми аппроксимируется истинная кривая y=f(x). Сам численный метод определяет порядок действий при переходе от данной точки кривой к следующей.
Дата добавления: 2015-11-18; просмотров: 1002;