ПОЛНОСВЯЗНЫЕ СЕТИ ХОПФИЛДА

Сеть Хопфилда (представлена на рис. 6.4) — однослойная сеть. Все нейроны связаны друг с другом связями w_ij , причем сигнал с выхода нейрона может подаваться на его же вход и необязательно w_ij = w_ji .

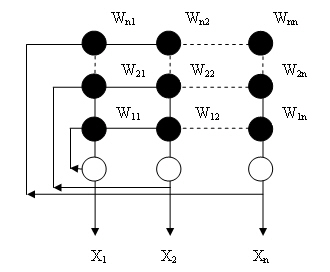
Рис. 6.4. Полносвязная сеть Хопфилда

Поскольку сигнал с выхода каждого нейрона подается на входы всех остальных, входной вектор начинает циркулировать, преобразуясь по сети до тех пор, пока сеть не придет в устойчивое состояние (то есть когда все нейроны на каждом последующем цикле будут вырабатывать тот же сигнал, что и на предыдущем). Очевидно, возможны случаи бесконечной циркуляции входного вектора без достижения устойчивого состояния.

Выберем функцию элементов в виде:

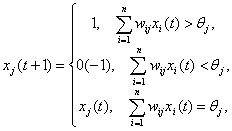
Состояние сети — множество текущих значений сигналов х от всех нейронов. Функционирование сети геометрически может быть представлено как движение вектора х , характеризующего состояние сети, на кубе [0,1]^п. Когда подается но вый входной вектор, сеть переходит из вершины в вершину, пока не стабилизируется. Устойчивая вершина определяется сетевыми весами, текущими входами и величиной порога. Если входной вектор частично неправилен или неполон, то сеть стабилизируется в вершине, ближайшей к желаемой.

В общем случае все возможные состояния сети образуют некое подобие холмистой поверхности, а текущие состояния сети аналогичны положениям тяжелого шарика, пущенного на эту поверхность, — он движется вниз по склону в ближайший локальный минимум. Каждая точка поверхности соответствует некоторому сочетанию активностей нейронов в сети, а высота подъема поверхности в данной точке характеризует «энергию» этого состояния. Энергия данного сочетания активностей определяется как сумма весов связей между парами активных нейронов, взятая со знаком минус (при 0 = 0).

Таким образом, если связь между двумя какими-то нейронами имеет большой положительный вес, то сочетания, в которых эти нейроны активны, характеризуются низким уровнем энергии — именно к таким сочетаниям и будет стремиться вся сеть. И, наоборот, нейроны с отрицательной связью при активации добавляют к энергии сети большую величину, так что сеть стремится избегать подобных состояний.

Динамику сети Хопфилда удобно описывать так называемой функцией энергии, которая в достаточно общем виде может быть определена как

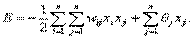
Функция энергии определяет устойчивость сети, другими словами — это функция Ляпунова сети Хопфилда , то есть функция, которая всегда убывает при изменении состояния сети. В конце концов эта функция должна достичь минимума и прекратить изменение, гарантируя тем самым устойчивость сети.

Изменение состояния какого-либо элемента сети всегда вызывает уменьшение энергии сети. Действительно, пусть изменил свое состояние элемент k ( k = 1 : n ) , то есть его состояние изменилось с +1 на 0 (или -1) или наоборот, тогда

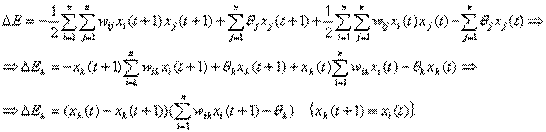
Видно, что в результате изменения k - ro элемента ∆ E_k ≤ 0, ∆ E_k = 0,, когда в сети не происходит никаких изменений. Благодаря такому непрерывному стремлению к уменьшению энергия, в конце концов, должна достигнуть минимума и прекратить изменение. По определению такая сеть является устойчивой. Сети Хопфил да называются также сетями, минимизирующими свою энергию. Сети Хопфилда имеют многочисленные применения. Некоторые из них связаны со способностью этих сетей запоминать , а затем восстанавливать даже по неполной входной информации различные образы. Другие применения связаны с возможностью использования сетей Хопфилда для решения оптимизационных задач.