МНОГОСЛОЙНЫЕ ОДНОНАПРАВЛЕННЫЕ СЕТИ
Такие сети называются также сетями прямого распространения,или многослойными персептронами.В дальнейшем (там, где это не может привести к неоднозначности) будем называть такие сети многослойными.
Сети этого типа состоят из нескольких слоев нейронов: входного слоя, выходного и нескольких «скрытых слоев». На рис. 6.3 изображена сеть, у которой К слоев. Нейроны каждого слоя не связаны между собой. Выходной сигнал с каждого нейрона поступает на входы всех нейронов следующего слоя. Нейроны входного слоя не осуществляют преобразования входных сигналов, их функция заключается в распределении этих сигналов между нейронами первого скрытого слоя.
Функционирование многослойной сети осуществляется следующим образом: входной сигнал, подаваемый на сеть, поступает на нейроны входного слоя, проходит по очереди через все слои и снимается с выходов нейронов выходного слоя. По мере распространения сигнала по сети он претерпевает ряд преобразований, которые зависят от его начального значения, от преобразующих функций и величин весов связей.
Пусть сеть состоит из К слоев: одного входного, одного выходного и (K >-2) скрытых слоев, — каждый слой состоит из n ( k ) нейронов. Набор выходных сигналов нейронов k - ro слоя ( k = 1: K ) обозначим . Далее обозначим wk набор весов синаптических связей, соединяющих нейроны k - 1-го слоя с нейронами k -го слоя; 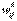 — вес связи, соединяющий i - й нейрон k -1-го слоя c j -м нейроном k -го слоя
— вес связи, соединяющий i - й нейрон k -1-го слоя c j -м нейроном k -го слоя 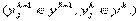 Т огда прямое функционирование сети описывается следующими соотношениями:
Т огда прямое функционирование сети описывается следующими соотношениями:
y 1 = x
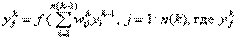 — выход нейронной сети.
— выход нейронной сети.
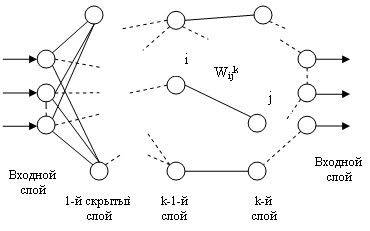
Рис 6.3. Схема многослойной однонаправленной сети
В основе методов обучения многослойных нейросетей наиболее часто лежит так называемое дельта-правило. Дельта-правило используется при обучении с учителем и реализуется следующим образом:
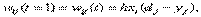 ,где
,где
h — параметр (шаг обучения);
d — эталонное (требуемое) значение выхода элемента.
Таким образом, изменение силы связей происходит в соответствии с ошибкой выходного сигнала 5 = ( d — у) и уровнем активности входного элемента х.. Обобщение дельта-правила , называемое обратным распространением ошибки ( Back — propagation ), применимо к сетям с любым числом слоев.
Обучение сети в этом случае состоит из следующих шагов:
1. Выбрать очередную обучающую пару ( х , d ). Подать входной вектор на вход сети.
2. Вычислить выход сети у.
3. Вычислить разность между выходом сети и требуемым выходом (ошибку).
4. Подкорректировать веса сети так, чтобы минимизировать ошибку.
5. Повторять шаги с 1-го по 4-й для каждой обучающей пары, пока ошибка не достигнет приемлемого уровня.
Ошибка функционирования сети обычно определяется как
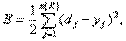 ,где
,где
у j =  — выход сети.
— выход сети.
Для уменьшения этой ошибки следует изменить веса сети по правилу
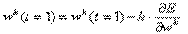
Эта формула описывает процесс градиентного спуска в пространстве весов. Очевидно, для выходного слоя

Так как
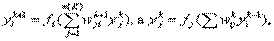
то для промежуточных (скрытых)слоев (то есть для
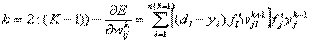
Если в качестве нелинейной преобразующей функции используется сигмоидная функция, то удобно использовать рекуррентные формулы:
 - для выходного слоя;
- для выходного слоя;
 - для скрытых cлоев,
- для скрытых cлоев,
тогда 
Эти соотношения называются формулами обратного распространения ошибки. Если при прямом функционировании входной сигнал распространяется по сети от входного слоя к выходному, то при подстройке весов ошибка сети распространяется от выходного слоя к входному.
Область применения многослойных нейросетей обусловлена тем, что они аппроксимируют отображение 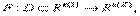 используя для этого предварительное обучение на наборах тренировочных данных (х 1 , d 1 ), ( x 2 , d 2 ), ..., ( xL , dL ), где de = F ( xe ). Таким образом, сеть можно рассматривать как модель у = φ ( х ) реального объекта у = F ( x ) . Доказаны теоремы о том, что с помощью сети с обратным распространением ошибок можно аппроксимировать любую функцию с любой точностью.
используя для этого предварительное обучение на наборах тренировочных данных (х 1 , d 1 ), ( x 2 , d 2 ), ..., ( xL , dL ), где de = F ( xe ). Таким образом, сеть можно рассматривать как модель у = φ ( х ) реального объекта у = F ( x ) . Доказаны теоремы о том, что с помощью сети с обратным распространением ошибок можно аппроксимировать любую функцию с любой точностью.
Дата добавления: 2015-11-18; просмотров: 1212;
