Режим обучения бинарными образами

Подадим на нейросеть три бинарных связи ( x _1, y ₁ ), ( x _2, y ₂ ), ( x _3, y ₃ ).

Пусть

x ₁ = (1,1,0,0) → y ₁ = (1,1,1,0);

x ₂ = (1,0,1,0) → у₂ = (0,1,0,1);

x ₃ = (1,0,0,1) → y ₃ = (0,1,0,0);

Смысл обучающих связей очевиден: если возбуждены нейроны a ₁ и а ₂ (в нашем распоряжении есть доллары), то по соответствующим синапсам возбудятся ней роны b ₁ , b ₂ , b ₃ (мы можем ими воспользоваться в США, России и Канаде), и т. д. От бинарных связей перейдем к биполярным (это сделано исключительно для простоты, чтобы не нужно было вводить ненулевой порог срабатывания нейронов):

x ₁ = (1,1-1,-1) → y ₁ = ( 1 ,1 -1,-1 );

x ₂ = ( 1,-11,-1 → у₂ = ( 1,-11,-1

x ₃ = ( 1,-1-1,1 → y ₃ = ( 1,-1-1,1 ;

Составим матрицу весов:

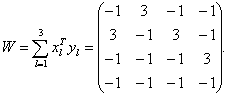
Режим распознавания.Оценим эффективность запоминания обучающих связей. Убедимся, что матрица W хранит связи ( x _1, y ₁ ), ( x _2, y ₂ ), ( x _3, y ₃ ). Подадим на вход x ₁ тогда x ₁ = (2, 2, 2, -2) — это означает, что в слое В возбудятся первые три нейрона (порог срабатывания принят равным нулю). Тогда в бинарной форме у = (1, 1, 1,0), что является требуемой ассоциацией. Это означает, что подача на вход x ₁ , приводит к y _1, то есть ЭВМ действительно «запомнила» связь ( x _1, y ₁ ). Аналогично проверяется запоминание остальных связей.

Сеть является двунаправленной: y ₁ W ^T = (1, 5, -3, -3) → (1, 1, 0, 0) → x ₁ , и т. д. Определим энергию связей в памяти:

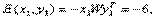аналогично Е( х₂, у₂) - 4 и Е(х₃ у₃) = -2. Следует ожидать, что при ошибке в исходной информации связь ( x _1, y ₁ ) будет притягивать к себе больше образов, так как это точка устойчивого равновесия с минимальным энергетическим уровнем. Действительно, подадим на вход образ x ' = (1,1,0,1) — искаженный на один бит x ₁ и х₃ тогда x ' W = (1,1,1, -3)→ (1,1,1,0) → y ₁ . Аналогично, если взять х " = (1, О, 1, 1) — вектор, расположенный «между» х ₂ и х_3, то получим (-3, 1, -3, 1) → (0, 1, 0, 1) → у₂ — связь ( x _2, y ₂ ) , притягивает к себе, так как ее энергия меньше энергии ( x _3, y ₃ ).

Работа с неопределенными данными. Рассмотрим случай, когда тип валюты неопределен x '- (1,0, 0,0), тогда x ' W = (-1, 3, -1, -1) → (0, 1, 0, 0) → у₃. Это означает, что она может быть использована только в той стране, где в ходу любая валюта.

Если валюта может быть любой, например, доллары и марки, то она может использоваться везде:

x '-(1, 1, 1,0) → x 'М = (1, 1,1,1) → у^’.

Проведенное исследование показывает, что построенная нейросеть способна за помнить необходимую информацию на этапе обучения, а в рабочем режиме позволяет решать задачи распознавания, то есть реализует функции ассоциативной памяти. Вся полученная при обучении информация сосредоточена в матрице W . За счет параллельной структуры сеть решает задачу «мгновенно» — за одно действие — умножение входного вектора на матрицу памяти. Так как информация как бы интегрирована в матрицу W , сеть способна достаточно эффективно решать задачу и при частичных искажениях в исходных данных.