Модель және модельдеу туралы негізгі түсінік

2-ші дәрісте қарастырылатын сұрақтар:

1. Модель және модельдеу туралы негізгі түсінік.

2. MS Excel - де оңтайластыру есептерін шығарудағы алғашқы қадамдар.

3. Компьютермен оңтайлы шешімдерді іздеу кезіндегі жасалатын типтік жұмыстар. Инструменттер панелі. Деректерді енгізу және форматтау әдістері. Көшірудің және тасымалдаудың негізгі мақсаттары.

Нақтылы объектілерді оқып, зерттеу нәтижесінде олардың әртүрлі қасиеттері және бір-бірімен арақатынастары жөнінде адам- да бір пікір қалыптасады. Осы зерттеу объекті туралы қалыптасқан көзқарасы бойынша адам оны суреттейді, ол үшін арнайы суреттеу тілі қолданылады. Суреттеу тілі сөзбен (вербальдық модельдер), математикалық формулалар, суреттер, сызбалар, графиктер, макет-тер және т.б. болуы мүмкін. Осылардың барлығын тұжырымдап модель деп, ал модельдерді тұрғызып, олардың шешімін іздеу жұмыстарын модельдеу деп атайтыны бәрімізге белгілі [1,2,3 және т.б.].

Модельдеу – нақтылы өмірдегі құбылыстарды және үрдістер-ді оқып, зерделейтін әмбебап тәсіл. Қазіргі ақпараттық техноло-гиялар дамыған заманда, бірден тура зерттеуге жатпайтын объекті-лерді оқып, зерделу үшін оны модельдеу ерекше маңызды. Мо-дельдеу шешім қабылдау жұмыстарында айрықша өзекті мәселеге айналды. Қазіргі кезде математикалық әдістермен модельдерді кеңінен пайдалану арқылы «Шешім қабылдау» теориясы дамыды және қалыптасты.

Математикалық әдістер және модельдер бірнеше пәндер жиынтығы екені жоғарыда айтылды. Солардың ішінен аграрлық жүйеде шешім қабылдауда көп қолданылатыны сызықтық про-граммалау әдістері (СП).

СП модельдері мақсат функциядан, шектеулер жүйелерінен және айнымалылардың теріс болмау шартынан тұратыны белгілі. Дегенменде, СП модельдерінің қысқаша математикалық формула-лары мен ондағы көрсеткіштерді тағыда еске түсірейік.

Экстремальды (яғни максимальды немесе минимальды) мәні ізелінетін математикалық өрнек мақсат функция деп аталады, мысалға,

Z =

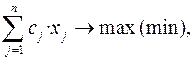
мұндағы c_j – мақсат функция коэффициенті.

Айнымалыларды теңдік және теңсіздік түрінде байланыс-тыратын математикалық өрнекті шектеу деп атайды. Барлық шектеулер есептің шектеулер жүйесін құрайды.

Шектеулер үш түрлі болуы мүмкін: теңдік (=), көп емес немесе тең типті теңсіздік түрінде (≤), кем емес немесе тең типті теңсіздік түрінде (≥). Мысалға,

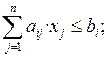
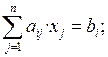
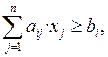
мұндағы i = 1, 2, … , m; a_ij – айнымалылар коэффициенттері (мұндағы индекс i – шектеулер нөмірі, индекс j – айнымалылар нөмірі), b_i – бос мүшелер (шектеулердің оң жағы) индекс i – шектеулер нөмірі.

Айнымалылардың теріс болмау шарты мына түрде жазы-лады:

x_j ≥ 0, j = 1, 2, …, n немесе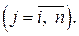

СП модельдерінің жалпы стандартты жазылу түрі:

– мақсат функцияның максимальды мәні ізделінсе

Z = 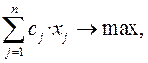(1.1)

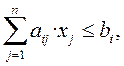i = 1,…, m немесе 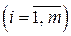, (1.2)

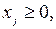j = 1, …, n немесе 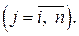(1.3)

– мақсат функцияның минимальды мәні ізделінсе

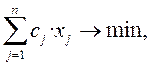Z = (1.4)

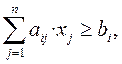i = 1, …, m немесе 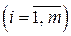(1.5)

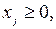j = 1,…,n немесе 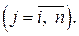(1.6)

Айнымалылар саны – n және шектеулер саны – m мен анық-талынатын оңтайластыру есептерінің өлшем бірлігі, оның маңызды сипаттамасы. Сондықтан шешім қабылдау үшін тәжірибелік жағдайда өндірістік есептерді құрған кезде осы екі көрсеткіштер қатысына ерекше көңіл аударған жөн. Егер n < m, онда есептің шешімі жоқ; n = m – есептің жалғыз ғана шешімі болады, яғни оңтайластрудың мағынасы болмайды; n > m – есептің шешімі өте көп есеп мағыналы деп саналады.

Егер есептің барлық шектеулері теңсіздік түрінде болса, онда оңтайластыру есебі барлық жағдайда мағыналы. Себебі негізгі х_i айнымалылар саны (n) теңсіздіктерді теңдікке түрлендіре-тін қосымша у_i айнымалылар санына, яғни шектеулер (m) санына (N=n+m) өседі. Нәтижесінде, барлық жағдайда: N = n+m > m, яғни есептің шешімі өтекөп болады.

Сонымен, N = n + k >m шартының орындалуы оңтайлаудың негізгі талабы екенін әрқашанда есте ұстағанымыз жөн. Мұндағы k–шектеулер жүйелеріндегі теңсіздіктер саны.

СП модельдерін шешу әдістері туралы [12, 15, 16 және 19] әдебиеттерде кеңінен жан-жақты баяндалған. Сондықтан оқу құра-лында қарастырылатын модельдердің математикалық теорясына және шешу әдістеріне көп көңіл аударылмайды. Біздің негізгі мақсат «Шешім қабылдау» мәселесінде белгілі математикалық әдістермен модельдерді қалай қолданады, яғни осы тұрғыда олар келесі бөлімдерде қарастырылады.

3-дәрістің мазмұны