Поиск решения в Excel
Цель работы:научиться использовать процессор Excel
для решения задач оптимизации
Содержание работы:
1 Создание формы
2 Ввод данных в окно Поиск решения
3 Задание параметров поиска и решение задачи
Математический аппарат Excel позволяет решать задачи линейного, нелинейного и целочисленного программирования. При этом оптимизация решения выполняется методом поиска решения, который запускается командой Сервис\Поиск решения.
Задача линейного программирования (ЗЛП) в общем случае формулируется следующим образом:
Определить максимум (минимум) целевой функции F max(min) при заданной системе ограничений (2) и граничных условий (3):
Fmax(min) =A1*X1+A2*X2+...+An*Xn (1)

B11*X1+B12*X2+...+B1n*Xn<=C1
B21*X1+B22*X2+...+B2n*Xn<=C2
............................ .................................. (2)
Bn1*X1+Bn2*X2+...+Bnn*Xn<=Cn
Xi>=0, i=1...n (3)
Рассмотрим применение табличного процессора Excel для решения ЗЛП на примере.
Задача. МП выпускает товары Х1,Х2,Х3,Х4, получая от реализации каждого прибыль в 60,70,120,130 руб. соответственно. Затраты на производство приведены в табл. 1. Определить:
1 Максимум прибыли в зависимости от оптимального распределения затрат.
2 Минимум ресурсов, необходимых для получения максимальной прибыли.
Таблица 1
| Затраты | Х1 | Х2 | Х3 | Х4 | Всего |
| Трудовые | |||||
| Сырьевые | |||||
| Финансы |
Составим математическую модель процесса по описанию задачи:
60Х1+70Х2+120Х3+130Х4 = Fmax – целевая функция прибыли.
 Х1+Х2+Х3+Х4 <= 16
Х1+Х2+Х3+Х4 <= 16
6Х1+5Х2+4Х3+Х4 <= 110 - ограничения модели
4Х1+6Х2+10Х3+13Х4 <= 100
Хj >=0 - граничные условия модели
Решение задачи средствами Excel состоит из 3 этапов:
1 Создание формы для ввода условий задачи, ввод в неё исходных данных и зависимостей из математической модели.
2 Ввод данных из формы в окно Поиск решения из меню Сервис.
3 Задание параметров поиска и решение задачи.
Создание формы
а)Составление формы в виде (рис. 1):
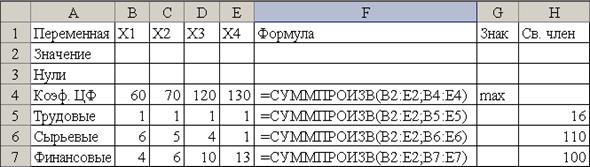
Рисунок 1 Форма для ввода данных ЗЛП
б)Запись в ячейки В4:Е4 коэффициентов целевой функции F (1),
в В5:Е7 коэффициентов из системы ограничений (2) и в ячейки Н5:Н7 - свободных членов из системы (2).
в)Ввод формул с помощью процедуры Мастер функций.
Для целевой функции: щелкнуть левой клавишей мыши по ячейке F4, затем по значку Мастера функций fх на панели инструментов, в появившемся окне Мастер функций, Шаг 1 в левой части выбрать категорию Математические, в правой части- функцию СУММПРОИЗВ, нажать
клавишу Далее, в окне Мастер функций, Шаг 2 в поле Массив 1 вве-
сти с клавиатуры В2:Е2 (ячейки, в которых будут варьироваться Х1..Х4), в поле Массив 2 ввести В4:Е4 (коэффициенты целевой функции ЦФ).
Примечание. Можно вводить В2:Е2 не с клавиатуры, а поставить курсор в окно Массив 1, а затем протащить курсор при нажатой левой клавише мыши по ячейкам В2:Е2, имена ячеек сами запишутся в окно. Аналогично поступить с полем Массив 2.
Нажать клавишу Готово, в ячейку F4 запишется формула 60*Х1+70*Х2+120*Х3+ 130*Х4 в виде СУММПРОИЗВ(В2:Е2)(В4:Е4)
Для левых частей ограничений аналогично:
- в ячейку F5 вносим СУММПРОИЗВ(В2:Е2)(В5:Е5),
- в ячейку F6 вносим СУММПРОИЗВ(В2:Е2)(В6:Е6),
- в ячейку F7 вносим СУММПРОИЗВ(В2:Е2)(В7:Е7).
Примечание. Чтобы каждый раз для новой ячейки F5..F7 не вызывать Мастер функций, можно скопировать в буфер команду из F4 СУММПРОИЗВ(B$2:E$2)(B4:E4) кнопкой на панели инструментов Копировать в буфер или командой из пункта меню Правка, затем вставить в выделенную ячейку F5.. F7 эту команду с помощью кнопки Вставить из буфера или соответствующей команды из пункта меню Правка, при этом ячейки B$2:E$2 не изменятся, а В4:Е4 поменяются на В5:Е5, В6:Е6 и В7:Е7, т.к. символ абсолютной адресации строк $ в них не введён.
Дата добавления: 2015-11-10; просмотров: 901;
