Программы ветвления
Пример 1
Составить программу и вывести на печать значения функции
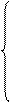
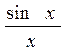 , если х = 0
, если х = 0
y =
1 в остальных случаях
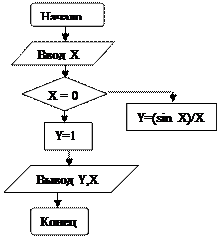
Составим схему алгоритма (рис. 1):
Блок 1 – начало алгоритма.
Блок 2 - ввод численного значения переменной Х.
Блок 3 - проверяется условие х=0. Если это условие выполняется, то дальнейшее вычисление пойдет по выходу "да" и в блоке 4 вычисляется
значение функции У=(sin (Х)/Х. Если условие Х=0 не выполняется, т.е.
значение переменной Х отлично от нуля, то дальнейшее вычисление
пойдет по выходу "нет" из логического блока 2 и в блоке 5 вычисляется значение функции У=1.
В блоке 6 предусмотрен вывод значений переменных У, Х.
Схема алгоритма Программa, вариант 1
CLS
INPUT X
IF X=0 THEN Y=SIN(X)/X ELSE Y=1
PRINT "Y=".Y,"X=".X
END
или вариант 2:
CLS
INPUT X
IF X=0 THEN Y= SIN(X)/X : GOTO М1
Y=1
Рисунок 1 Cхема алгоритма M1: PRINT "Y=";Y,"X=”;X
END
Работа программы(построчно), вариант 1:
Очистка экрана.
Оператором INPUT X вводится значение аргумента Х.
Проверяется условие – если(IF) Х = 0, то(THEN) У вычисляется по формуле Y=SIN(X)/X, иначе (ELZE) У = 1.
Выводятся на экран значения У и Х.
Конец программы.
Вариант 2:
Очистка экрана.
Ввод Х.
Проверка условия – если Х=0, тогда У вычисляется по формуле Y=SIN(X)/X и оператором безусловного перехода GOTO управление передаётся метке М1, т.е. печати У и Х. Если этого перехода не сделать, то следующим оператором параметр Y переопределится, т.е.ему присвоится другое значение (Y =1), а вычисленное значение Y потеряется.
Если условие не выполняется, то программа переходит к следующему оператору У=1, к печати Y и Х и программа заканчивается (Конец)..
Пример 2
Составить программу и вывести на печать значение функции у.
y = max {a,min{b,c}}
Словесный алгоритм:
По условию задачи надо найти сначала наименьшую из переменных b и с, а потом сравнить её на максимум с величиной а и результат присвоить переменной у.
Программа:
CLS
INPUT"ВВЕСТИ a,b,c";a,b,c
IF b<c THEN u=b ELSE u=c
IF a>u THEN y=a ELSE y=u
PRINT"y="; у
END
Работа программы(построчно):
Очистка экрана.
Ввод значений a,b,c, через запятую.
Если b<c, то новой переменной u присваивается значение b, если нет, то значение с. Таким образом, вместо b и с теперь появилась величина u, причём равная наименьшему из b и с. Затем эта u сравнивается с переменной а на максимум, т.е. находится наибольшее значение между переменными a и u. Оно присваивается переменной у, которое и выводится на печать.
Пример 3
Составить программу и вывести на печать значение функции у.
y = max {a,b,c}
Программа:
CLS
INPUT"введите a,b,c"; a,b,c
IF a > b AND a > c THEN y = a
IF b > a AND b > c THEN y = b
IF c > a AND c > b THEN y = c
PRINT"y="; у
END
Описание программы:
для нахождения максимума последовательно сравниваются все
переменные:
- если а больше b и а больше с, то у = а,
- еслиb больше а и b больше с, то у = b,
- еслис больше а и с больше b, то у = а.
Затем значение у распечатывается и программа заканчивается.
Пример 4
Составить программу вычисления значения функции у.
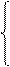 х + а, если х=10;
х + а, если х=10;
у = х - cz, если x<10;
x - a, если x>10.
Программа:
Вариант 1 Вариант 2
| CLS INPUT a,x,c,z IF x = 10 THEN y =x + a IF x > 10 THEN y =x – c*z IF x < 10 THEN y = x - a PRINT"y="; у END | CLS INPUT a,x,c,z IF x = 10 THEN y =x + a IF x > 10 THEN y =x – c*z ELSE y = x - a PRINT"y="; у END |
В варианте №2 для второго условия можно использовать оператор IF…THEN…ELSE, т.к. после перебора вариантов х=10 и х>10 не осталось никаких вариантов, кроме х<10.
Контрольные вопросы
1 Оператор безусловного перехода, его формат.
2. Операторы условного перехода, их форматы
3 Типовой алгоритм нахождения максимума или минимума нескольких величин.
4 Какими могут быть условия ветвления в условном операторе?
5 Как действует оператор безусловного перехода?
6 Правила использования метки для перехода в программе.
Задания
В вариантах задания требуется составить программу для нахождения максимумов или минимумов, но предварительно сравниваемые величины нужно вычислить.
| № вар. | Функция | Составляющие | Аргументы |
| v =min(a,b) | a=1/2 x 2y+3 + yx^2 -1; b =ln(x+y+3x +4)+e | x=1.24; y=2.35 | |
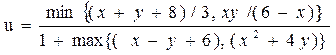
| x=-8.2; y=2.25 | ||
| w =min(max(a,b),c) | a = ln(ex-y +2|y|; c = 2sin(x2 -6x)
b= 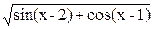
| x=3.2; y=1.32 |
| z =min(a,b) | a = |cos(x)+cos(y)|1+2x b = 1+ex+y +sin|4x-2| | x=-1.25; y=2.25 | ||
| m = max(a,b) | a = sin(x+y2)+ex+1;
b = 
| x=2.32; y=-3.43 | ||
| u = max(a,min(b,c)) | a = 1/(1+x+y) +|x+y|;
b = 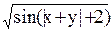 ;
c = cos(x+2)-2x; ;
c = cos(x+2)-2x;
| x=-2.32; y=3.3 | ||
| u = min(a,b) | a = ex+1 +sin(x2 -8);
b = 
| x=-4.28 | ||
| c = tg (min(a,b)) | a =  ;
b = sin(e0,5 +e4) ;
b = sin(e0,5 +e4)
| |||
| t = min{y,z} | y =|ln(1+x)5 +cos PIx3|; z = (cos ex +(1/x)+ex) sin x | x=1.09 | ||
| t = max{y,z,x} | y =cos PIx3 +ln(1+x)2; z = e2x +(1/x2)+cos5 x | x=1.78 | ||
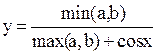
| a = sin x+x4 +ecos x; b =ln x7 +sin PIx2 | x=4.0 | ||
| y = max{z,t}5 | z = sin(ln x +sin PIx); t =x3 +sin x+ecos x | x - дано | ||
| u = min(max(a,b),c) | a = sin(x+y8)+ex+1; b = cos|x-y| + |x3-y|; c = x4+3y5+2; | x=-2.2 | ||
| u =min(a,max(b,c)) | a =e-x+1 +sin(x6 -8);
b = 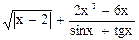 |x|;
c =e7x +6x-2 |x|;
c =e7x +6x-2
| x=-3.8 | ||
| a = max{t,min{y,z}} | y = 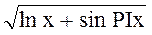 ;
z =(x +cos ex +sin x); t =x ;
z =(x +cos ex +sin x); t =x
| x=4.35 | ||
| u =man(a,b,c) | a=tg x 2y+3 + yx^2 -1; b =log(x+y+3x +4)+e; c=arctg(x-y)3; | x=1.24; y=2.35 | ||
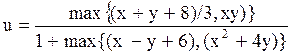
| x=-8.2; y=2.25 | |||
| u = min(max(a,b),c) | a = ln(ex-y +2|y|; b = sin(x-2)+cos (x-1); c = ctg(x2 -6x) | x=3.2; y=1.32 | ||
| u=max(a,b) | a = 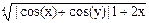 ; b = 1+ex+y +sin|4x-2| ; b = 1+ex+y +sin|4x-2|
| x =-1.25; y=2.25 | ||
| m = min(a,b) ·max(a,b) | a = sin(x+y2)+ex+1; b = ln(x-y)+log|x-y | | x=2.32; y=-3.43 | ||
Содержание отчета
1 Название, цель, содержание работы
2 Задание для своего варианта.
3 Схема алгоритма.
4 Программы.
5 Результаты расчётов в среде QB.
6 Письменные ответы на контрольные вопросы.
7 Выводы по работе
Лабораторная работа № 4.
Дата добавления: 2015-11-10; просмотров: 1316;
