ОПРЕДЕЛЕНИЕ ДЕБИТОВ ПРИ ЗАДАННЫХ ЗАБОЙНЫХ ДАВЛЕНИЯХ
ОПРЕДЕЛЕНИЕ ДЕБИТОВ И ДАВЛЕНИЙ
Изменение дебитов и забойных давлении определяют приближенным методом последовательной смены стационарных состояний либо по несколько уточненному способу [24].
В последнем случае дебит
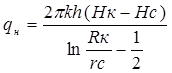(V.6)
Здесь Нк—Нс— разность обобщенных функций Христиановича при соответствующих давлениях на контуре рк и на скважине рс (остальные обозначения прежние),
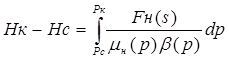(V.7)
Установлено [35], что подынтегральная функция в последнем выражении апроксимируется следующего вида зависимостью:
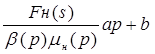(V.8)
Для определения разности обобщенных Функций Христиановича применяют приближенную зависимость, вытекающую из уравнений (V.7) и (V.8),
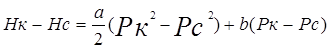(V.9)
Коэффициенты а и Ь определяют по формулам:
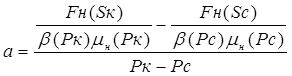(V.10)
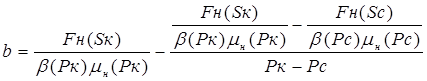(V.11)
ОПРЕДЕЛЕНИЕ ДЕБИТОВ ПРИ ЗАДАННЫХ ЗАБОЙНЫХ ДАВЛЕНИЯХ
Для заданных забойных давлений уравнение дебита (V.6) с учетом (V.8) можно записать в виде
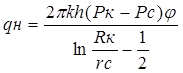, (V.12)
где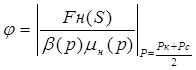 
(V.13)
Дебиты определяют следующим образом.
1. Из зависимости (V.2) для ряда последовательных значений sk находят соответствующие им значения рк.
2. Из условия постоянства газового фактора вдоль линии тока определяют Ψ(š):
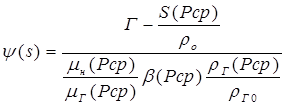(V.14)
где усредненное по пласту давление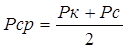 
š— соответствующее рср значение нефтенасыщенности; Г определяется по уравнению (V.3) при р == рк и s=sк.
3. По значениям Ψ(š) с помощью экспериментальных зависимостей или таблицы Царевича определим š и Fн (š), соответствующие последовательности выбранных значений sк.
4. По формулам (V.12) и (V. 13) определим дебит нефти для каждой пары значений sк и рк
5. Зная дебит нефти, определим дебит газа по формуле
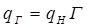(V. 15)
6. Изменения эксплуатационных характеристик во времени определим с помощью формулы
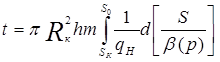(V. 16)
которая при помощи известных методов численного интегрирования легко преобразуется к виду
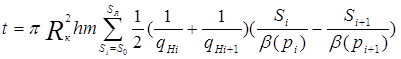(V. 17)
Если же заданы давления на забоях скважин или на линиях рядов на ту или иную дату, то тем самым заданы результаты сложения депрессий от отдельных скважин или их групп. В таких случаях следует определить исходные слагаемые qi, для чего требуется решить систему алгебраических уравнений первой степени, построенных по типу (VI .6). Это при большом числе неизвестных представляет определенные трудности ввиду трудоемкости вычислений с увеличением числа уравнений (неизвестных).
Необходимо отметить, что это можно сделать лишь заранее, приняв тот или иной закон изменения дебита, для которого решена первая задача (определение перепада по заданному дебиту), так как лишь в таком случае можно определить функцию Ψi. Кроме того, для соблюдения условия равенства давлений в какой-либо другой момент времени заданным величинам надо повторно решить систему уравнений.
Из задач этого типа решены только наиболее простые, причем многие из них только приближенно. Более или менее строго решена лишь задача определения дебитов круговых или бесконечных прямолинейных галерей, на которых заданы постоянные давления.
Дата добавления: 2015-11-10; просмотров: 1350;