Возрастание и убывание функций
ИССЛЕДОВАНИЕ ФУНКЦИЙ И ПОСТРОЕНИЕ ГРАФИКОВ
Одним из приложений производной является ее применение к исследованию функций, т.е. к характеристике поведения функции при изменении независимой переменной.
Возрастание и убывание функций
Согласно определению (п.1.12), функция 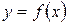 возрастает (убывает) на интервале
возрастает (убывает) на интервале 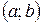 , если большему значению аргумента х из этого интервала соответствует большее (меньшее) значение функции у.
, если большему значению аргумента х из этого интервала соответствует большее (меньшее) значение функции у.
Из определения следует, что для возрастающей функции приращение функции 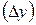 и приращение аргумента
и приращение аргумента 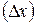 имеют одинаковые знаки, и следовательно, их отношение положительно, т.е.
имеют одинаковые знаки, и следовательно, их отношение положительно, т.е.
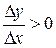 .
.
Для убывающей функции 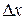 и
и 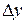 имеют противоположные знаки, в силу чего, отношение приращений отрицательно:
имеют противоположные знаки, в силу чего, отношение приращений отрицательно:
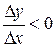 .
.
Если функция в интервале 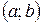 дифференцируема, то, переходя в неравенствах к пределу при
дифференцируема, то, переходя в неравенствах к пределу при 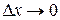 , получим:
, получим:
− для возрастающей в интервале 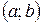 функции
функции
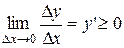 ;
;
− для убывающей в интервале 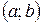 функции
функции
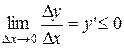 .
.
Сформулируем необходимые и достаточные условия возрастания и убывания функции.
Теорема(необходимые условия).
Если дифференцируемая на интервале 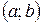 функция
функция 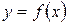 возрастает (убывает), то ее производная
возрастает (убывает), то ее производная 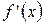 неотрицательна:
неотрицательна: 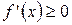 (неположительна:
(неположительна: 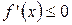 ) для всех
) для всех 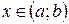 .
.
Геометрически эта теорема означает, что касательные к графику возрастающей функции образуют острые углы ( 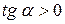 ) с положительным направлением оси Ох (рис. 5.1), а касательные к графику убывающей функции − тупые углы (
) с положительным направлением оси Ох (рис. 5.1), а касательные к графику убывающей функции − тупые углы ( 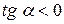 ) (рис. 5.2).
) (рис. 5.2).
Теорема(достаточные условия).
Если функция 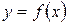 дифференцируема на интервале
дифференцируема на интервале 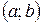 и ее производная положительна:
и ее производная положительна: 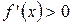 (отрицательна:
(отрицательна: 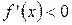 ) для всех
) для всех 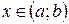 , то эта функция возрастает (убывает) на интервале
, то эта функция возрастает (убывает) на интервале 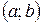 .
.
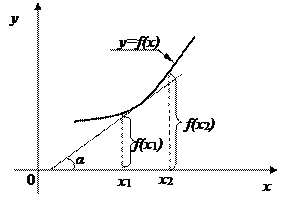 |
Рис. 5.1
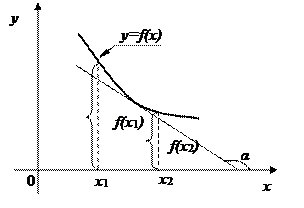 |
Рис. 5.2
Таким образом, изучение вопроса об участках возрастания или убывания дифференцируемой функции 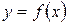 сводится к исследованию знака первой производной этой функции.
сводится к исследованию знака первой производной этой функции.
Пример
Найти интервалы возрастания и убывания функции: 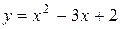 .
.
Функция определена на всей числовой оси.
Имеем 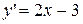 ;
; 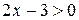 ;
; 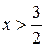 .
.
Следовательно, функция возрастает (« ↑ ») в интервале 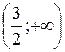 .
.
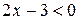 ;
; 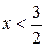 .
.
Функция убывает (« ↓ ») в интервале 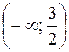 .
.
Дата добавления: 2015-11-10; просмотров: 1460;
