Производная обратной функции. Если и − взаимо-обратные дифференцируемые функции и , то
Если 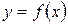 и
и 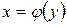 − взаимо-обратные дифференцируемые функции и
− взаимо-обратные дифференцируемые функции и 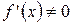 , то
, то
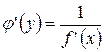 или
или 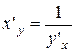 ,
,
т.е. производная обратной функции равна обратной величине производной данной функции.
Записывают:
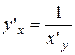 или
или 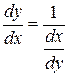 .
.
Пример
Найти производную функции 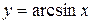 .
.
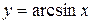 ,
, 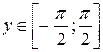 , тогда
, тогда 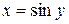 ,
, 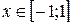 . Имеем
. Имеем 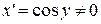 .
.
 .
.
Итак, 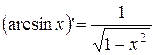 .
.
Таблица производных
Для удобства и упрощения процесса дифференцирования формулы производных основных элементарных функций и правила дифференцирования сведены в таблицу.
| Правила дифференцирования | Формулы дифференцирования | ||
| 1. | 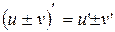
| 1. | 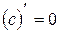 , , 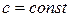
|
| 2. | 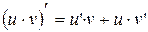
| 2. | 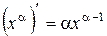
|
| 3. | 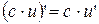 , , 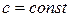
| 3. | 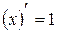
|
| 4. | 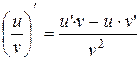 , , 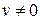 . .
| 4. | 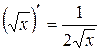
|
| 5. | 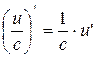 , , 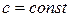
| 5. | 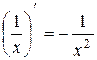
|
| 6. | 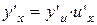 ,
если ,
если 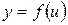 , , 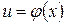
| 6. | 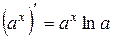
|
| 7. | 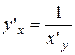 ,
если ,
если 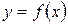 , , 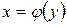
| 7. | 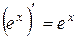
|
| 8. | 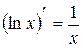
| ||
| 9. | 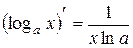
| ||
| 10. | 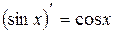
| ||
| 11. | 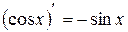
| ||
| 12. | 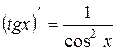
| ||
| 13. | 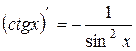
| ||
| 14. | 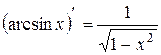
| ||
| 15. | 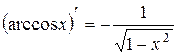
| ||
| 16. | 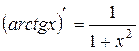
| ||
| 17. | 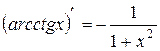
|
Примеры отыскания производных сложных функций
На практике чаще всего приходится находить производные от сложных функций. Покажем на примерах, как находить производные от таких функций.
1. 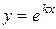 , k − число.
, k − число.
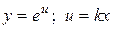 ;
;
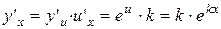 .
.
2. 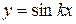 .
.
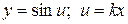 ;
;
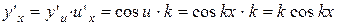 .
.
3. 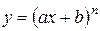 .
.
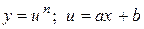 ;
;
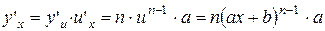 .
.
4. 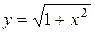 .
.
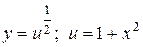 ;
;
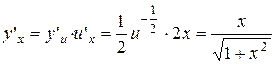 .
.
5. 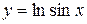 .
.
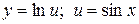 ;
;
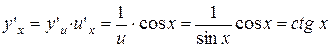 .
.
6. 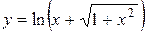 .
.
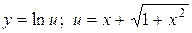 ;
;
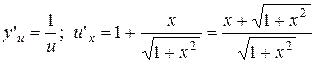 ;
;
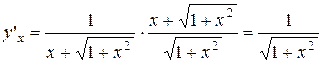 .
.
7. 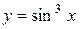 .
.
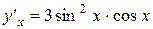 .
.
8. 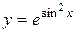 .
.
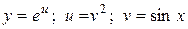 ;
;
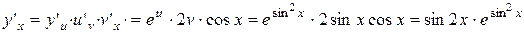 .
.
9. 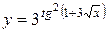 .
.
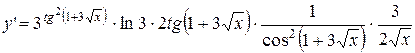 .
.
10. 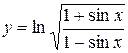 .
.
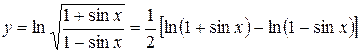 ;
;
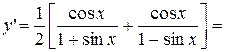
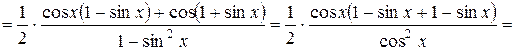
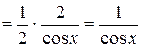 .
.
Для случая дифференцирования сложных функций, таблицу производных можно переписать в более общем виде.
Формулы дифференцирования основных элементарных функций от промежуточного аргумента 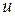 (
( 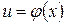 )
)
| 1. | 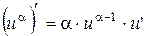
| 2. | 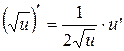
|
| 3. | 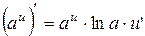
| 4. | 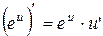
|
| 5. | 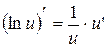
| 6. | 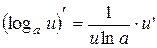
|
| 7. | 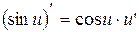
| 8. | 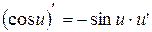
|
| 9. | 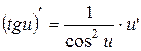
| 10. | 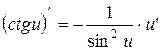
|
| 11. | 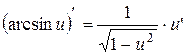
| 12. | 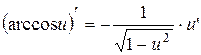
|
| 13. | 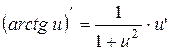
| 14. | 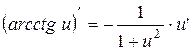
|
Дата добавления: 2015-11-10; просмотров: 611;
