Измерение преимуществ в эмпирических системах
Квазишкалы и эмпирические системы.Эмпирической системой U называется множество А={x1,…,xn} альтернатив и отношение Р с носителем А, U=<A,P>. В процессе измерений каждой альтернативе xi ÎА ставиться в соответствие определенное число, то есть проводиться измерение эмпирической системы, в результате чего определяется соответствующая к ней числовая система Uz=<Az,Pz>, где Аz={z1,…,zn} – множество чисел, полученное путем применения отображения f:А® Аz, то есть zj=f(xj).
Таким образом эмпирическая система U отображается гомоморфной с сохранением справедливости условий 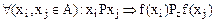 в числовую систему. Если в эмпирической системе отношение Р отображает преимущества альтернативы, то Рz естественно рассматривать как в множестве чисел Аz.
в числовую систему. Если в эмпирической системе отношение Р отображает преимущества альтернативы, то Рz естественно рассматривать как в множестве чисел Аz.
Шкалой измерений называется тройка <U,f,Uz>. При каждом измерении используется шкала определенного типа.
Отношение Р эмпирической системы U=<A,P> при условии наличия несравнимых альтернатив является отношением порядка. Далее будем считать, что первичное отношение Р уже факторизовано по эквивалентности, то есть все существующие альтернативы разные, таким образом, приписывая определенное число в шкале или квазишкале мы присваиваем его значение всем альтернативам первичного отношения, которые эквивалентны между собой.
В множестве альтернатив А можно выделить связанные подмножества (подмножество связанное, если связным является отношение, которое определенно на этом подмножестве). Связное подмножество AiÌA ,будет максимальное, если для любого 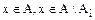 множество
множество 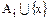 будет несвязным.
будет несвязным.
Проблемы отображения эмпирической системы в числовой. 1. Существует ли числовая система Uz, в которую гомоморфно отображается U, то есть может ли быть «измерена» эмпирическая система? Ответ: да, потому что, возможность измерения основных типов эмпиричных систем, которая рассматривается в экспертных оценках, доказана. 2. Проблема связанна с существованием большого количества способов отображения одной и той же эмпирической системы с отношениями в разнообразные числовые системы и основывается в определении множества таких систем. Для такого множества числовых систем характерным является вид преобразования, который отображает одну числовую систему в другую числовую систему. Например существуют три шкалы измерения температуры: Цельсия, Кельвина и Фаренгейта, при этом переход от одной к другой осуществляется с помощью линейного преобразования y=ax+b, a>0. Таким образом линейное преобразование результатов измерения температуры не искажает смысла измерений. 3. Теория измерений – проблема адекватности – основывается на определении возможности осуществления определенных действий (операций) над числовыми оценками альтернатив без искажения полученной определенной информации (сравнение по значениям, сложение, умножение и т.д.). Тип шкалы измерений определяется допустимым преобразованием числовой системы, которая отображает ее в другую числовую систему, которая так как и предыдущая, является гомоморфным образом первичной эмпирической системы. Для основных типов шкал множество допустимых преобразований простирается от тождественного преобразования до произвольного взаимнооднозначного преобразования.
Для обеспечения полноты рассмотрения вводится понятие промежуточной качественной шкалы, которая использует больше информации, чем порядковая, но меньше чем шкала интервалов – шкалы гиперпорядка. В гипер упорядочиваниях ранжируются не альтернативы, а разности оценок альтернатив.
Относительно транзитивности – то настолько жесткое условие не накладывается на экспертные результаты в виде эмпирического отношения, а оно используется непосредственно в дальнейших операциях или апроксимируется ближайшим в определенном смысле транзитивным отношением. Кроме того, нарушение транзитивности используется для оценивания степени последовательности размышлений эксперта – чем больше она нарушается, тем менее последовательным считается эксперт. Таким образом проблемы, которые возникают при переходе от эмпирических систем к отношениям, решаются частично на этапе формирования порядка опроса эксперта, а частично – путем аппроксимации эмпиричных результатов отношениям заданного типа.
Дата добавления: 2015-09-11; просмотров: 1068;
