Меры близости и метризованные отношения.
Виды метризованных отношений. Основной вид экспертной информации о преимуществах во множестве альтернатив - это информация в виде эмпирических отношений, которые получены в процессе опроса экспертов. Отношения, полученные путем экспертного опроса, могут иметь такие свойства, как связность, транзитивность и т.д., а могут их и не иметь. С другой стороны свойства результирующего отношения могут быть известны a-priori, а результаты опросов экспертов в виде отношений этих свойств не иметь. В таком случае возникает задача аппроксимации полученного отношения ближайшем в определенном смысле отношением с заданными свойствами.
Метризованные отношения PM являются двойкой PM=<P,M(P)>, где Р – бинарное отношение, 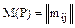 , где
, где 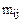 - число, которое характеризирует степень преимущества альтернативы xi над альтернативой xj, или в случае толерантности степень сходства этих альтернатив. Метризованные отношения PM=<P,M(P)> называется рефлексивным, антирефлексивным, симметричным, асимметричным, антисимметричным, транзитивным, если отношение Р имеет соответственные свойства. Свойство транзитивности по сравнению с неметризованными отношениями усиливается.
- число, которое характеризирует степень преимущества альтернативы xi над альтернативой xj, или в случае толерантности степень сходства этих альтернатив. Метризованные отношения PM=<P,M(P)> называется рефлексивным, антирефлексивным, симметричным, асимметричным, антисимметричным, транзитивным, если отношение Р имеет соответственные свойства. Свойство транзитивности по сравнению с неметризованными отношениями усиливается.
Самыми распространенными типами метризованных отношений являются аддитивный и мультипликативный.
Аддитивным называется метризованное отношение, для которого выполняется условие
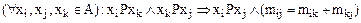 ,
,
где А – носитель Р.
Мльтипликативным называется метризованное отношение, для которого справедливо условие
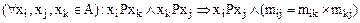
Для аддитивных метризованных отношений 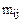 показывает, «на сколько» альтернатива xi лучше, чем xj, для мультипликативных – «во сколько раз». PM будем называть метризованным отношением частичного порядка, линейного порядка, толерантности или эквивалентности, если отношение Р имеет соответствующие свойства.
показывает, «на сколько» альтернатива xi лучше, чем xj, для мультипликативных – «во сколько раз». PM будем называть метризованным отношением частичного порядка, линейного порядка, толерантности или эквивалентности, если отношение Р имеет соответствующие свойства.
Элементы метризованного отношения PM могут быть поданы несколькими способами. Представление в виде двойки PM=<P,M(P)>, в виде одной матрицы 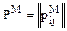 . Если PM – метризованное отношение частичного порядка, значение элементов
. Если PM – метризованное отношение частичного порядка, значение элементов 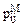 определяются следующим образом:
определяются следующим образом:
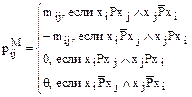
где 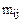 - число, которое показывает, на сколько xi лучше, чем xj. Если альтернативы xi и xj равноценны (эквивалентны), то
- число, которое показывает, на сколько xi лучше, чем xj. Если альтернативы xi и xj равноценны (эквивалентны), то 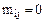 , если несравнимые – то соответственно символ
, если несравнимые – то соответственно символ 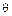 , получая в случае необходимости информацию о равноценности или несравнимости альтернатив непосредственно из матрицы Р.
, получая в случае необходимости информацию о равноценности или несравнимости альтернатив непосредственно из матрицы Р.
Матрица метризованного отношения частичного (а так же линейного) порядка будет согласованной, если будет обратно симметричной, то есть 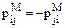 . В этом случае0=-0 и
. В этом случае0=-0 и 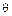 =-
=- 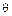 . Согласованная матрица – это идеальный случай. На самом деле эмпирическая матрица будет иметь определенный уровень несогласованности сравнимо с идеальным случаем.
. Согласованная матрица – это идеальный случай. На самом деле эмпирическая матрица будет иметь определенный уровень несогласованности сравнимо с идеальным случаем.
Для мультипликативных метризованных отношений частичного или линейного порядка, 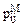 целесообразно определить следующим образом:
целесообразно определить следующим образом:
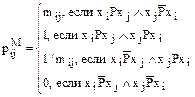
где 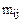 - число, указанное экспертом, которое показывает во сколько раз xi лучше, чем xj.
- число, указанное экспертом, которое показывает во сколько раз xi лучше, чем xj.
Кроме этого в этой форме можно представить и неметризованные бинарные отношения Р:
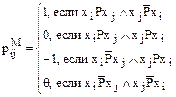
что является эквивалентным представлением матрицы Р.
Такое представление имеет предпочтение, потому что появляется возможность оперировать лишь матрицей 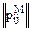 без использования матрицы Р соответственного неметризованного бинарного отношения.
без использования матрицы Р соответственного неметризованного бинарного отношения.
Когда 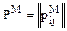 является отношением толерантности или эквивалентности, то
является отношением толерантности или эквивалентности, то 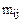 измеряют степень подобности альтернатив xi и xj, и
измеряют степень подобности альтернатив xi и xj, и
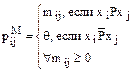 ,
,
и соответственная матрица РМ является симметричной.
Метризованные отношения не только позволяют в числовой форме отобразить степень предпочтения одной альтернативы над другой с точки зрения ЛПР, но и предопределяют целый ряд вопросов: каким образом оценить близость или несоответствия утверждений экспертов, имея результаты в виде бинарных отношений?; каким эталонным бинарным отношением лучше аппроксимирует эмпирическое отношение, полученное в результате опроса экспертов?; какие действия можно выполнять с полученными экспертными результатами в форме метризованных бинарных отношений, а какие нет?; какие процедуры следует использовать для получения числовой информации о преимуществах в множестве альтернатив от эксперта?; каким образом оценить надежность и непротиворечивость эксперта?.
Дата добавления: 2015-09-11; просмотров: 1090;
