Прямолинейно-параллельный фильтрационный поток упругой жидкости
ОДНОМЕРНЫЕ ФИЛЬТРАЦИОННЫЕ ПОТОКИ УПРУГОЙ ЖИДКОСТИ. ТОЧНЫЕ РЕШЕНИЯ УРАВНЕНИЯ ПЬЕЗОПРОВОДНОСТИ. ОСНОВНАЯ ФОРМУЛА ТЕОРИИ УПРУГОГО РЕЖИМА
Рассмотрим наиболее простые точные решения уравнения пьезопроводности (5.14) для одномерных потоков.
Прямолинейно-параллельный фильтрационный поток упругой жидкости
Случай 1. Пусть в полубесконечном горизонтальном пласте постоянной толщины h и ширины В начальное пластовое давление всюду постоянно и равно рк На галерее (при х = 0) давление мгновенно снижено до рг и в дальнейшем поддерживается постоянным (т.е. рг = const). В удаленных точках (х → ∞) давление в любой момент времени остается равным рк
В пласте образуется неустановившийся прямолинейно-параллельный поток упругой жидкости. Давление в любой точке потока х и в любой момент времени t можно определить, интегрируя уравнение Фурье (5.21):
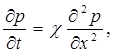0 < х < ∞ (5.28)
Начальные и граничные условия при этом будут следующие:
р{х, t) = рк при t=0;
р(х, t) = рг при х = 0, t > 0;
р(х, t) = рк при х = ∞, t ≥ 0. (5.29)
Задача заключается в определении дебита галереи Q(t) и давления в любой точке потока и в любой момент времени р(х, t).
Используя анализ размерностей, покажем, что поставленная задача автомодельна, т. е. из аргументов, от которых зависит давление, можно составить один (безразмерный) комплекс.
Обозначим через Р =(р— рг)/(рк — рг) безразмерное давление, которое, как следует из соотношений (5.28) и (5.29), зависит от времени t, координаты х и коэффициента пьезопроводности т. е.
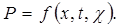
Размерности этих аргументов следующие: [х] = L, [t] = Т,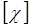 
= L2 T-1, и из них можно составить один безразмерный комплекс 
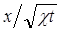. Приняв за новую переменную величину 
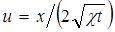, сведем задачу к нахождению безразмерного давления Р, зависящего только от u: P=f(u). При этом условия (5.29) переходят в следующие:
Р = 0 при u = 0;
Р = 1 при u = ∞, (5.30)
В силу линейности дифференциального уравнения (5.28) для функции Р имеем такое же уравнение
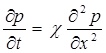, (5.31)
По правилу дифференцирования сложных функций находим:
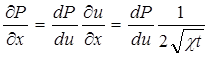, где 
;
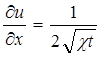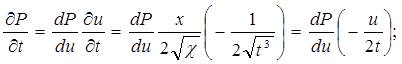
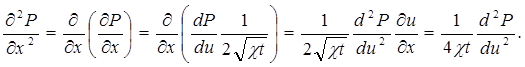
Подставляя найденные значения производных в уравнение (5.31), получим обыкновенное дифференциальное уравнение
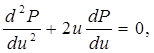(5.32)
которое должно быть решено при условиях (5.30).
Для решения уравнения (5.32) обозначим:
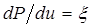
тогда уравнение (5.32) принимает вид
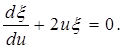(5.33)
Разделив переменные в (5.33) и проинтегрировав, получим:
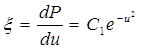, (5.34)
где С1 - постоянная интегрирования.
Проинтегрировав (5.34), получим:
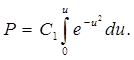
Здесь использовано первое из условий (5.30).
Второе условие (5.30) дает: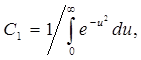 
но из интегрального
исчисления известно, что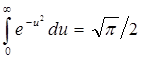 
, поэтому
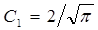, и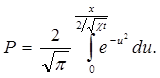 
(5.35)
Интеграл (5.35) называется интегралом вероятности и является табулированной функцией, изменяющейся в пределах от 0 до 1:
 |
Рис. 5.1. Кривые распределения давления в различные моменты времени внеустановившемся прямолинейно-параллельном потоке упругой жидкости при условии Рг = const
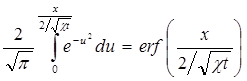
Таким образом
.
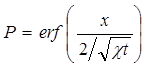Тогда закон распределения давления в неустановившемся прямолинейно-параллельном фильтрационном потоке упругой жидкости имеет вид
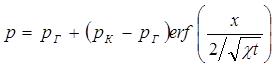(5.36)
Типичные кривые распределения давления в различные моменты времени в неустановившемся прямолинейно-параллельном потоке упругой жидкости в галерее, пущенной в эксплуатацию с постоянным забойным давлением рг = const, приведены на рис. 5.1. Найдем дебит галереи Q. Будем считать положительным дебит, отбираемый из галереи (х = 0), когда поток движется против оси х и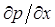 
> 0. Согласно закону Дарси
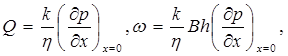(5.37)
где В, h -соответственно ширина и толщина пласта.
Продифференцировав выражение (5.36), получим:
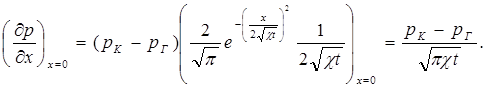(5.38)
Дебит галереи в любой момент времени найдем, подставив значение градиента давления 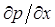из (5.38) в выражение (5.37):
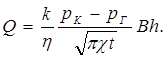(5.39)
 |
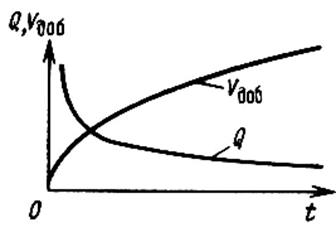Puс. 5.2. Зависимости дебита и добычи, жидкости от времени после пуска галереи при условии рг = const
Из формулы (5.39) следует, что дебит галереи убывает с течением времени как 1/√t и при t → ∞ стремится к нулю. В начальный момент времени формула (5.39) дает бесконечное значение, что является следствием скачка давления на галерее (от pk до рг ) в этот момент времени.
Накопленная к моменту t добыча Vдоб определяется по формуле:
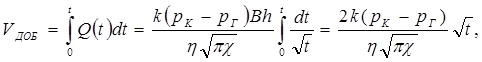
т.е. сразу после начала отбора из галереи она быстро возрастает, а в дальнейшем растет очень медленно (рис. 5,2).
Случай 2. В таком же полубесконечном пласте, что и в случае 1, в момент времени t = 0 пущена в эксплуатацию галерея с постоянным объемным дебитом Q. Требуется найти давление в любой точке пласта
в любой момент времени.
Математически задача заключается в интегрировании уравнения
(5.21) при следующих начальных и граничных условиях:
р (х, t) = рк при t=0;
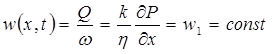при х = 0;
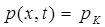при х = ¥ (5.40)
Умножив обе части уравнения (5.21) на k/η и продифференцировав по х, получим:
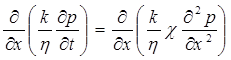
или
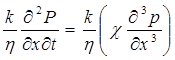
откуда, меняя порядок дифференцирования, получим:
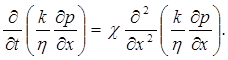(5.41)
Так как
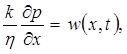
то уравнение (5.41) можно переписать в следующем виде:
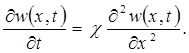(5.42)
Полученное уравнение (5.42) по форме совпадает с уравнением теплопроводности (5.21). Следовательно, решением уравнения (5.42) будет решение, аналогичное (5.36), с заменой давления р на скорость фильтрации w:
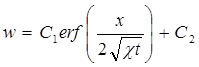, (5.43)
При этом следует иметь в виду, что начальное и граничное условия для w имеют вид:
w(x, 0) = 0, w(0, t)=w1.
Отсюда C2 = w1, C1 = - w1 и, следовательно,
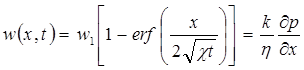(5.44)
Для того, чтобы найти распределение давления в потоке, необходимо проинтегрировать уравнение (5.44) по x, полагая, что время t фиксировано.
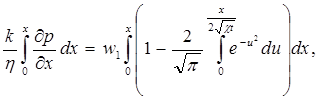
откуда
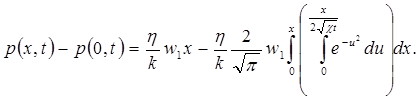(5.45)
Последнее слагаемое в (5.45) интегрируется по частям, в результате
чего находим:
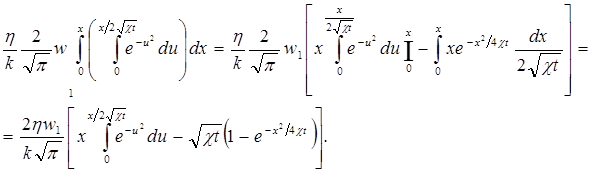
Тогда уравнение (5.45) можно записать следующим образом:
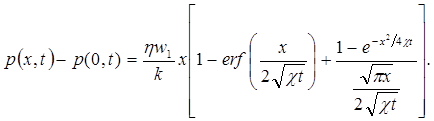(5.46)
С учетом того. что р (0, t) есть давление на галерее, т. е. р (0, t) = pг (t), из (5.46) запишем выражение для давления в любой точке потока:
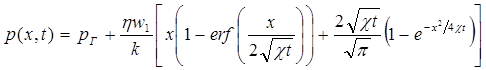, (5.47)
Для того, чтобы найти закон изменения давления на галерее pг (t), подставим в (5.47) граничное условие р(х, t) =pк при х → ∞. Так как при
х → ∞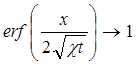 
, то произведение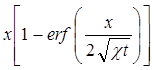 
дает неопределенность вида ∞. Раскрывая ее по правилу Лопиталя, можно показать, что это произведение стремится к нулю; учитывая также, что
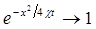при x → ∞, получаем:
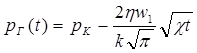
или
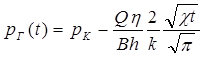. (5.48)
Дата добавления: 2015-11-10; просмотров: 3208;