Шифрование с помощью аналитических преобразований

Достаточно надежное закрытие информации может быть обеспечено при использовании для шифрования некоторых аналитических преобразований. Для этого можно использовать методы алгебры матриц, например умножение матрицы на вектор по правилу:

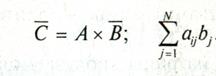
Если матрицу А = (аij) использовать в качестве ключа, а вместо

компонента вектора В= (bj) подставить символы текста, то компоненты вектора С= (сj) будут представлять собой символы зашифрованного текста.

Приведем пример, взяв в качестве ключа квадратную матрицу третьего порядка

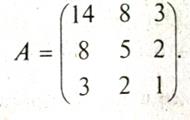
Заменим буквы алфавита цифрами, соответствующими их порядковому номеру в алфавите: А — О, Б — 1, В — 2 и т. д. Тогда отрывку текста BATAЛA будет соответствовать последовательность 2, О, 19, О, 12, О. По принятому алгоритму шифрования выполним необходимые действия

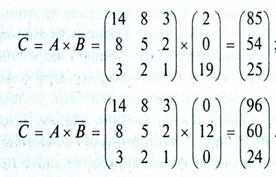
При этом зашифрованный текст будет иметь вид: 85, 54 25, 96, 60, 24.

Дешифрование осуществляется с использованием того же правила умножения матрицы на вектор, только в качестве ключа берется матрица, обратная той, с помощью которой осуществляется шифрование, а в качестве вектора-сомножителя — соответствующие фрагменты символов закрытого текста; тогда значениями вектора-результата будут цифровые эквиваленты знаков открытого текста.

Матрицей, обратной данной А, называется матрица А^-1, получающая из присоединенной матрицы делением всех ее элементов на определитель данной матрицы. В свою очередь присоединенной называется матрица, составленная из алгебраических дополнений А_ij, к элементам данной матрицы, которые вычисляются по формуле:

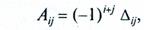
Определителем матрицы называется алгебраическая сумма n! членов (для определителя итого порядка), составленная следующим образом: членами служат всевозможные произведения n элементов матрицы, взятых по одному в каждой строке и в каждом столбце, причем член суммы берется со знаком «+», если его индексы составляют четную подстановку, и со знаком « — » — в противоположном случае. Для матрицы третьего порядка, например, определитель вычисляется следующим образом: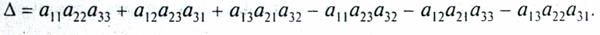

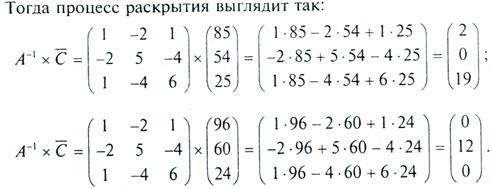
Таким образом, получена последовательность знаков раскрытого текста 2, О, 19, О, 12, О, что соответствует исходному тексту. Этот метод шифрования является формальным, что позволяет легко реализовать его программными средствами.