Пример 2. В турнире участвуют 8 игроков

В турнире участвуют 8 игроков. Каким количеством способов могут распределяться три первых места? (Сколько вариантов "тройки призеров" существует в данном случае?)

Решение.

Тройка призеров – это три имени из восьми, расположенные в определенном порядке.

.

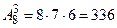Можно также рассматривать размещения элементов из неограниченного количества предметов, относящихся к различным сортам (предметы одного сорта не различаются).

Размещения с повторениями из элементов по

Пусть имеется бесконечное множество элементов, относящихся к различным видам (предметы одного сорта не различаются).

Размещением с повторениями из элементов по называется выборка расположенных в определенном порядке элементов из неограниченного количества элементов различных сортов. Такие выборки называются расстановками. Две расстановки считаются различными, если они отличаются либо элементами, либо порядком их следования.

Количество таких размещений обозначается и вычисляется по формуле:

.

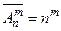Докажем справедливость этой формулы методом математической индукции.

Пусть 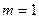. Каждое размещение состоит из одного элемента. Различные размещения получатся, если брать элементы разных сортов, число которых равно . Следовательно, .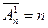

Предположим, что 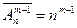. Рассмотрим фиксированное размещение 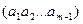и припишем к нему элемент 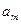одного из видов. В результате из одного фиксированного размещения, состоящего из 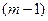элементов получим размещений, содержащих элементов. Учитывая, что число таких фиксированных размещений из 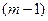элементов равно 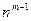, получим, что число размещений из элементов по с повторениями равно .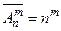

В этой формуле, также как в формуле для 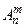, ровно сомножителей, но все они равны , так как количество способов выбора элемента на второе, третье и т.д. место остается равным , а не убывает, как в предыдущем случае.