Размещения

Пусть задано множество В, состоящее из элементов.

Размещениями из элементов по называются упорядоченные подмножества элементов из , которые отличаются друг от друга либо хотя бы одним элементом либо порядком расположения элементов.

Число размещений обозначается 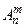и вычисляется по формуле:

.

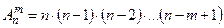Формула эта выводится по правилу произведения. Составим всевозможные размещения из элементов по , т.е. подмножества множества В, содержащие элементов. На первом шаге можно выбрать любой из имеющихся элементов, т.е. существует выборов из имеющихся элементов. Второй элемент в размещении можно выбрать из оставшихся 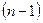элементов. Поэтому пару элементов можно выбрать 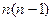способами, так как к каждому из первых элементов можно присоединить второй элемент способами. Третий элемент в размещении можно выбрать из оставшихся 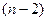элементов. Поэтому тройку элементов можно выбрать 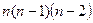способами. Продолжая этот процесс, получим, что число размещений из элементов по равно

.

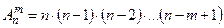Заметим, что в формуле ровно сомножителей, первый сомножитель равен , каждый следующий на единицу меньше.