Алгоритм составления оптимального маршрута
1. По исходным данным строится «минимальное дерево». Центры потреблению распределяются таким образом, чтобы из исходного графа получилось дерево без замкнутых циклов.
- Центры потребления разбиваются на 2 и более группы (в зависимости от исходных данных, то есть количества продукции и грузоподъемности транспортного средства) таким образом, чтобы в каждой группе сумма потребляемой продукции в пунктах была одинаковой (возможен вариант приблизительно одинаковой).
- Для каждой группы поочередно строится таблица-матрица минимальных расстояний по исходному графу. Элементами матрицы являются кратчайшие расстояния от склада (Ц) до пунктов потребления (при этом перебираются все возможные варианты).
- Значения матрицы суммируются по столбцам, и из этих значений выбирается 3 наибольших. По этим пунктам строится начальный маршрут.
- Для пунктов, не вошедших в начальный маршрут (обозначаются i) поочередно определяется разница (начиная с наибольшего значения суммы по столбцу) длины расстояний от пунктов по следующей формуле:
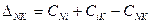 , где N – начальный пункт, К – конечный пункт.
, где N – начальный пункт, К – конечный пункт. - Из этой разницы выбирается минимальная, и данный пункт вставляется в начальный маршрут между пунктами, где была получена эта разница. Строится новый маршрут.
- В полученный новый маршрут по п.5 и 6 вставляются все оставшиеся пункты.
- По окончательному маршруту перевозки считается длина пути.
Пример 1. В таблице задан граф пунктов потребления продукции. Также указано расстояние от каждого пункта и количество потребляемой продукции. Всего продукции на складе 300 контейнеров, грузоподъемность транспортного средства 150 контейнеров. За минимальное количество рейсов и с минимальным пробегом транспортного средства распределите продукцию от склада до пунктов потребления.
| Пункт потребления | A | B | C | D | E | K | L | M | N | O | P | Q | R | S | Центр |
| Кол-во продукции | |||||||||||||||
| Расстояние | Ц-А | А-В | B-D | B-S | S-D | S-P | D-P | D-C | A-C | К-M | Ц-M | Ц-R | M-N | N-O | R-O |
| 2,0 | 3,0 | 4,0 | 7,0 | 9,0 | 8,0 | 7,0 | 5,0 | 6,0 | 12,0 | 11,0 | 14,0 | 15,0 | 19,0 | 4,0 |
| N-L | O-L | C-K | P-Q | Q-L | C-E | D-E | P-E | E-K | K-L | Q-K |
| 15,0 | 10,0 | 12,0 | 8,0 | 3,0 | 9,0 | 12,0 | 8,0 | 11,0 | 10,0 | 10,0 |
Планирование маршрута доставки груза в смешанном сообщении на основе сетевого графика
Снижение транспортных расходов возможно за счет применения новых технологий перевозки, реорганизации транспортной инфраструктуры и интеграции транспортных систем. Таким образом, главным инструментом в указанном процессе является использование нескольких видов транспорта при доставке грузов.
Смешанная перевозка – транспортировка грузовой партии от пункта отправления до пункта назначения, когда в процессе перемещения используется более одного вида транспорта. Для планирования смешанной перевозки грузов наиболее актуальным является использование сетевых моделей. Задача сетевого планирования сводится к построению рационального плана проведения сложного комплекса работ, состоящего из отдельных элементарных взаимно обусловленных операций. Сетевой график позволяет изобразить логическую и временную структуру комплекса работ. Работы на графике изображаются векторами (дугами). Моменты завершения работ - это узлы графика (рис. 2). Дуге, идущей из i-го события в j-ое, присваивается время выполнения 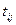 . В том случае, если точное время выполнения работ неизвестно, то, зная максимальное
. В том случае, если точное время выполнения работ неизвестно, то, зная максимальное 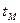 , минимальное
, минимальное 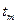 и наиболее вероятное
и наиболее вероятное 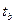 , можно определить:
, можно определить: 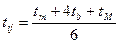 .
.
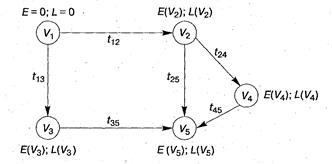
Рис.2
Предполагая, что исходное событие 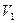 происходит в нулевой момент времени, определяют ранние сроки совершения событий
происходит в нулевой момент времени, определяют ранние сроки совершения событий 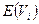 . Для исходного события
. Для исходного события 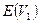 =0. Для остальных работ расчет производится исходя из следующих условий. Пусть в i-ое событие входит несколько работ, находятся все суммы
=0. Для остальных работ расчет производится исходя из следующих условий. Пусть в i-ое событие входит несколько работ, находятся все суммы 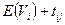 , выбирается максимальная сумма. Поздний срок наступления события
, выбирается максимальная сумма. Поздний срок наступления события 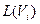 характеризует последний момент времени, в которых может произойти событие. Для последней работы
характеризует последний момент времени, в которых может произойти событие. Для последней работы 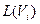 =
= 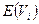 . Для нахождения всех остальных поздних сроков работ вычисляются все разности
. Для нахождения всех остальных поздних сроков работ вычисляются все разности 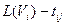 , выбирается минимальный. Путь, состоящий из работ, где совпадают ранние и поздние сроки выполнения, называется критическим.
, выбирается минимальный. Путь, состоящий из работ, где совпадают ранние и поздние сроки выполнения, называется критическим.
Общий резерв времени ( 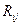 ) – это время, на которое можно перенести начало работы, не увеличивая общее время выполнения проекта.
) – это время, на которое можно перенести начало работы, не увеличивая общее время выполнения проекта. 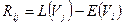 . Свободный резерв
. Свободный резерв 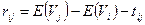 - показывает, насколько можно отодвинуть начало работы.
- показывает, насколько можно отодвинуть начало работы.
Транспортный процесс при смешанных перевозках состоит из последовательной доставки груза различными видами транспорта и промежуточной перегрузки.
При смешанных перевозках выбор варианта доставки осуществляется на основе следующих критериев:
Ø Время (T);
Ø Стоимость (С);
Ø Приведенная стоимость, определяемая по формуле: 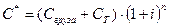 , где
, где 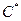 - оценка стоимости груза и его доставки с учетом фактора времени;
- оценка стоимости груза и его доставки с учетом фактора времени; 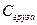 - закупочная стоимость груза;
- закупочная стоимость груза; 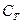 - стоимость перевозки;
- стоимость перевозки; 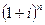 - множитель наращивания процентов по процентной ставке i за n периодов,
- множитель наращивания процентов по процентной ставке i за n периодов, 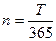 .
.
Каждой работе 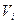 соответствуют три значения - время (Ti), стоимость доставки (Ci) и С*, которые определяются как сумма дуг по различным вариантам доставки. Условной работе
соответствуют три значения - время (Ti), стоимость доставки (Ci) и С*, которые определяются как сумма дуг по различным вариантам доставки. Условной работе 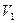 - соответствуют 3 значения, равные 0.
- соответствуют 3 значения, равные 0.
Пусть следования из одного узла в другой может быт альтернативным, например:
Ø Если дуга означает процесс транспортировки, то наличие двух и более путей свидетельствует о возможности использования на этом маршруте нескольких альтернативных друг другу видов транспорта;
Ø Если дуга означает процесс оформления груза в пункте, то привлечение посредников и отказ от их услуг приведут к появлению нескольких альтернативных друг другу вариантов.
Таким образом, для пунктов, где пересекаются альтернативные пути доставки, появляется несколько суммарных значений, например 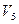 :
:
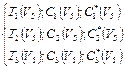 .
.
Выбор производится на основе одного определяющего на данный момент времени показателя. В случае, если важность показателей имеет примерно одинаковое значение и если ни для одной из схем доставки не оказалось, что все значения ниже, чем для любой другой, для выбора схемы перевозки можно использовать критерии принятия решения в условиях неопределенности. Наиболее известны критерии Лапласа, Вальда, Сэвиджа и Гурвица, позволяющие принять решение на основании матрицы возможных результатов: строки соответствуют возможным действиям 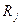 (варианты доставки груза); столбцы – возможным состоянием
(варианты доставки груза); столбцы – возможным состоянием 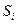 (критерии доставки); элементы матрицы – результат при выборе
(критерии доставки); элементы матрицы – результат при выборе 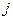 -го действия и реализации i-го состояния
-го действия и реализации i-го состояния 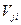 .
.
Дата добавления: 2015-08-21; просмотров: 2903;
