Теория удара.

При решении механических задач по законам сохранения можно не рассматривать промежуточных состояний системы, а сразу сравнить начальное и конечное состояния. Пример – идеальные удары – это столкновение двух или более тел, при котором взаимодействие длится очень короткое время. Понятие удара в физике имеет более широкое значение, которое может не предполагать непосредственного соприкосновения сталкивающихся объектов. (Например, можно говорить о столкновении молекул, хотя они взаимо-действуют на расстоянии через свои электрические поля). Особенностью теории столкновений является то, что мы детально не анализируем механизм взаимодействия, а рассматриваем значение кинетических энергий и импульсов до и после столкновения

Силы взаимодействия между сталкивающимися телами столь велики, что внешними силами, действующими на них, можно пренебречь. Это позволяет систему соударяющихся тел считать изолированной и применить к ней законы сохранения. При соударении тел друг с другом они претерпевают деформации. При этом кинетическая энергия, которой обладали тела до удара, частично или полностью переходит в потенциальную энергию упругой деформации и внутреннюю энергию тел.

а) Абсолютно упругий центральный удар 2-х шаров (скорость направлена по линии центров масс).

При абсолютно упругом ударе тела после взаимодействия полностью восстанавливают свою форму, механическая энергия тел не переходит в другие не механические виды энергии - полная механическая энергия тел сохраняется. В момент удара кинетическая энергия переходит полностью или частично в потенциальную энергию упругой деформации. Затем тела восстанавливают первоначальную форму, и в итоге, потенциальная энергия упругой деформации снова переходит в кинетическую энергию. Тела разлетаются со скоростями, величина и направление которых определяется двумя условиями – сохранением полной механической энергии и импульса системы тел.

При центральном ударе соударение может произойти, если 1) шары движутся на встречу друг другу и 2) один из шаров догоняет другой.

1)

2)

Заданы массы m₁, m₂ и скорости V₁ и V₂ направленные по их линии центров.

После абсолютно упругого удара шары получают скорости U₁ и U₂ направленные вдоль той же линии. По закону сохранения импульса:

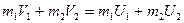
По закону сохранения энергии:

Это система 2-х уравнений с 2-мя неизвестными, решив которую получим:

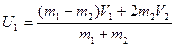
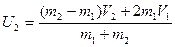…(4.14)

Отметим, что скорости шаров после абсолютно упругого удара не могут быть одинаковыми – приняв U₁=U₂ из (4.14) Þ V₁ = V₂то есть, для этого необходимо чтобы они были одинаковыми и до удара, но в этом случае соударение не может произойти. Отсюда следует, что условие равенства скоростей шаров после удара не совместимо с законом сохранения энергии.

Если взять равными массы соударяющихся шаров m₁ = m₂ то из (4.14) Þ что при этом условии U₁ = V₂, а U₂ = V₁. То есть шары при соударении обмениваются скоростями. Например, если первый шар до соударения покоится, то после удара он движется с той же скоростью, какую имел до удара второй шар, второй же шар после удара оказывается неподвижным.

б) Абсолютно неупругий центральный удар. При абсолютно неупругом ударе тела после взаимодействия движутся как одно целое; либо покоятся. Кинетическая энергия тел полностью или частично превращается во внутреннюю энергию. После такого удара, тела слипаются, т.к. нет сил, восстанавливающих форму тел и Þ их расталкивающих. При абсолютно не упругом ударе выполняется лишь закон сохранения импульса, закон же сохранения механической энергии не соблюдается.

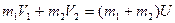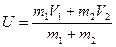Новая общая скорость И может быть найдена по закону сохранения импульса: Þ …(4.15)

Часть механической энергии переходит во внутреннюю. По закону сохранения и превращения энергии можно узнать эти «потери»:

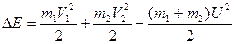…(4.16)