Решение матричных уравнений
Рассмотрим систему n линейных алгебраических уравнений относительно n неизвестных х1, х2, …, хn:

В соответствии с правилом умножения матриц рассмотренная система линейных уравнений может быть записана в матричном виде Ах = b,
где: 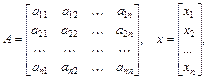
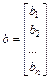
Матрица А, столбцами которой являются коэффициенты при соответствующих неизвестных, а строками – коэффициенты при неизвестных в соответствующем уравнении, называется матрицей системы; матрица-столбец b, элементами которой являются правые части уравнений системы, называется матрицей правой части или просто правой частью системы. Матрица-столбец х, элементы которой - искомые неизвестные, называется решением системы.
Если матрица А - неособенная, то есть det A ¹ 0 то система (2), или эквивалентное ей матричное уравнение (3), имеет единственное решение. В самом деле, при условии det A ¹ 0 существует обратная матрица А-1. Умножая обе части уравнения (3) на матрицу А-1 получим: 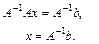
Эта формула дает решение матричного уравнения и оно единственно.
Системы линейных уравнений удобно решать с помощью функции lsolve.
lsolve(А, b)–Возвращается вектор решения x такой, что Ах = b.
Аргументы:
А - квадратная, не сингулярная матрица.
b - вектор, имеющий столько же рядов, сколько рядов в матрице А.
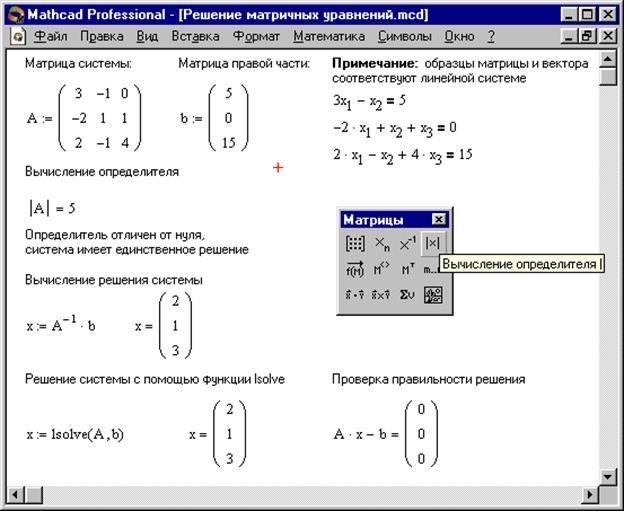 На Рисунке 8 показано решение системы трех линейных уравнений относительно трех неизвестных.
На Рисунке 8 показано решение системы трех линейных уравнений относительно трех неизвестных.
Рисунок 7. Решение матричных уравнений
Дата добавления: 2015-08-21; просмотров: 961;
