Коэффициент корреляции знаков Фехнера
К простейшим показателям степени тесноты связи относят коэффициент корреляции знаков, который был предложен немецким ученым Г.Фехнером (1801-1887). Этот показатель основан на оценке степени согласованности направлений отклонений индивидуальных значений факторного и результативного признаков от соответствующих средних. Для его расчета вычисляют средние значения результативного и факторного признаков, а затем проставляют знаки отклонений для всех значений взаимосвязанных пар признаков.
Если ввести обозначения: na – число совпадений знаков отклонений индивидуальных величин от средней, nb – число несовпадений знаков отклонений, то коэффициент Фехнера можно записать таким образом:
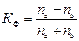 (1.1)
(1.1)
Коэффициент Фехнера может принимать различные значения в пределах от –1 до +1. Если знаки всех отклонений совпадут, то nb = 0 и тогда показатель будет равен +1, что свидетельствует о возможном наличии прямой связи. Если же знаки всех отклонений будут разными, тогда na = 0 и коэффициент Фехнера будет равен –1, что дает основание предположить наличие обратной связи.
Рассмотрим расчет КФ на примере, приведенном в табл.1.2.
Средний размер затрат на рекламу по всем 20 фирмам составит 9,95 усл. ден. ед., а среднее число туристов, воспользовавшихся услугами фирмы, – 952 человека. В графах 4 и 5 табл.1.2 указаны знаки отклонений значений признаков от соответствующей средней.
| Порядковый номер фирмы | Затраты на рекламу xi, усл. ден. ед. | Количество туристов, воспользовавшихся услугами фирмы yi, человек | Знаки отклонений индивидуальных значений признака от средней | Совпадение (а) или несовпадение (b) знаков | |
| для xi | для yi | ||||
| – | – | а | |||
| – | – | а | |||
| – | – | а | |||
| – | – | а | |||
| – | – | а | |||
| – | – | а | |||
| – | – | а | |||
| – | – | а | |||
| + | – | b | |||
| + | + | а | |||
| + | – | b | |||
| + | + | а | |||
| + | – | b | |||
| + | – | b | |||
| + | + | а | |||
| + | + | а | |||
| + | + | а | |||
| + | + | а | |||
| + | + | а | |||
| + | + | а |
Подсчитав число совпадений знаков na = 16 и число несовпадений знаков nb = 4 (см. графу 6 табл.1.2), рассчитаем коэффициент Фехнера по формуле (1.1):
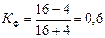
Полученная величина коэффициента Фехнера свидетельствует о том, что можно предполагать наличие прямой зависимости между исследуемыми признаками.
Как видно из приведенной формулы для расчета коэффициента Фехнера, величина этого показателя не зависит от величины отклонений факторного и результативного признака от соответствующей средней величины. Поэтому нельзя говорить о степени тесноты корреляционной связи, а тем более об оценке ее существенности на основании только коэффициента Фехнера. При малом объеме исходной информации коэффициент Фехнера практически решает ту же задачу, которая ставится при построении групповых и корреляционных таблиц, т.е. отвечает на вопрос о наличии и направлении корреляционной связи между признаками. В том случае, если построена корреляционная или же групповая таблица, дополнительный расчет коэффициента Фехнера не имеет практической ценности.
Дата добавления: 2015-08-21; просмотров: 696;
