Дросселирование, как способ понижения температуры.

В общих чертах процесс дросселирования рассматривался в лекции 5. В ней этот процесс представлен был как предельный случай течения газовых сред в каналах с большими скоростями. Предельность заключалась в том, что вся работа проталкивания через малое отверстие тратится на необратимый процесс роста энтропии. Так как теплота диссипации остается в самом потоке, то инвариантом процесса дросселирования является величина энтальпии: h = const. В той же лекции 5 показано, что давление в процессе уменьшается, удельный объем, соответственно, увеличивается, энтропия растет. Зато вопрос об изменении температуры остался открытым.

Займемся этим вопросом сейчас. По существу речь идет о знаке

(∂T/∂p)_h ,

причем в этой частной производной определенно знаем, что знак знаменателя отрицателен. Следовательно, если определим знак самой производной, то найдем знак ее числителя, т.е. узнаем характер изменения температуры в процессе: растет или убывает.

Выше в наших лекциях было показано, что для реальных веществ

dh = Tds + vdp, dh = c_pdT – (T(∂v/∂T)_p – v)dp. (7.1)

Для дросселирования h = const, т.е. dh = 0, поэтому

0 = c_pdT – (T(∂v/∂T)_p – v)dp.

Разделим обе части этого уравнения на dp (еще раз подчеркнем, что dp < 0) и будем помнить, что h = const, т.е.

(∂T/∂p)_h = 1/c_p [T(∂v/∂T)_p – v] или (∂T/∂p)_h = T/c_p [(∂v/∂T)_p – v/T] = α_h. (7.2)

Величина α_h в термодинамике носит название дифференциального дроссельэффекта Джоуля – Томсона. Знак этой величины по существу и определяет знак приращения ΔT при дросселировании. Рассмотрим рис. 7.1.

Рис. 7.1. К определению знака изменения температуры при дросселировании.

На рис 7.1 изображена изобара p = const в осях T – v. Для реальных веществ ее, как правило, строят экспериментально. Рассматривается точка А на изобаре. Эта точка характеризует состояние реального рабочего тела далеко от самого дросселя (т.е. резкого сужения или малого отверстия в мембране поперек трубы, по которой происходит течение газа). Ставится вопрос: температура за дросселем станет больше или меньше температуры в точке А? Глядя на формулу (7.2), видно, что T > 0 всегда, с_р > 0 тоже. Следовательно, знак α_h определяется знаком выражения в квадратных скобках. Найдем его для точки А. Проводим касательную к изобаре в точке А. Тогда tgφ = (∂T/∂v)_p. В соответствии с теоремой о производной обратной функции tg(π/2 – φ) = (∂v/∂T)_p.

Далее, соединим точку А с началом системы координат О и рассмотрим прямоугольный треугольник ОАv. Отношение v/T (см.(7.2)) есть tgæ, причем угол æ накрест лежащий углу АОТ_А и, следовательно, ему равный.

Сравнивая величину углов π/2 – φ и æ видно, что первый угол меньше второго, следовательно, (∂v/∂T)_h в точке А на рис.7.1 меньше, чем отношение v/T в той же точке. Следовательно, выражение в квадратной скобке в формуле (7.2) отрицательно, тогда и α_h < 0 и, окончательно, приращение температуры после дросселирования положительно. Иными словами, если до дросселя была температура T_А, то после дросселя будет большая температура.

Рассматривая рис. 7.1 и проводя аналогичные построения, можно доказать, что, если до дросселя была температура T_В (см. точку В на рис. 7.1), то после процесса дросселирования температура рабочего тела уменьшится.

Если при дросселировании из точки А температура увеличивается, а при дросселировании из точки В уменьшается, то должна существовать точка С на изобаре, при дросселировании из которой температура не изменится. И действительно, проведя из начала координат О прямую, касательную к изобаре, получим точку С (см. рис. 7.2) В ней

(∂v/∂T)_h = v/T,

тогда α_h = (∂T/∂p)_h = 0 и, следовательно, T = const.

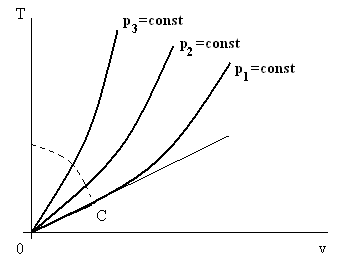
Рис. 7.2. Иллюстрация к определению точки инверсии и линии инверсии.

Линия инверсии изображена пунктиром.

Определение.Состояние рабочего тела до процесса дросселирования, при котором после этого процесса температура не изменяется, называется состоянием инверсии, а сама точка, характеризующая это состояние, называется точкой инверсии.

Согласно этому определению точка С на рис. 7.2 является точкой инверсии. Если в координатах T – v изобразить пучок изобар, на каждой найти точку инверсии и все эти точки соединить плавной линией, то получим геометрическое место точек инверсии (см. пунктирную линию на рис. 7.2). Если дросселировать рассматриваемое вещество из состояний, точки которых расположены правее и выше линии инверсии, то температура рабочего тела после дросселя обязательно будет выше температуры до дросселя. Если эти точки будут располагаться ниже линии инверсии, то – ниже.